
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Strain rate
Strain rate is the quantity of strain in unit time : unit in s-1
An elongation of 1% in one second gives a strain rate of 10-2 s-1
Geological strain rates (crust, mantle) are on the order of 10-12 to 10-14 s-1, very far from what can be reproduced using laboratory experiments (the slowest experiments are on the order of 10-8 s-1 in which 1% of strain is obtained in 106 seconds, about 100 days).
3. Stress
Stress can be viewed as an « oriented pressure ». By contrast to body forces whose magnitude depends on the volume or mass (represented by gravity or inertia), stress is a consequence of surface forces. Stress is reponsible for rock deformation.
No stress, no deformation. Stress may be due to the overburden (the load of rocks), such as the compaction of sediments that become transformed into rocks, but more generally to « tectonic » stress.
Let us consider first the lithostatic pressure, which is isotropic (Plitho = r.g.h), non oriented, hence is not a stress. This lithostatic pressure increases (indefinitely) with depth, and this pressure is applied to every material element, whatever its orientation in space. P is mesaured in MPa (1 MPa = 10 bars = 0.01 kb ; or 1 kb = 100 MPa) sometimes in GPa at great depth. Lithostatic pressure may be represented as a sphere whose diameter regularly increases with depth (Figure).

Figure : Increase of the isotropic part of the stress (lithostatic pressure), and decrease of the differential stress with increasing depth. In A1, at shallow depth : low isotropic -lithostatic- pressure (Plitho = r g Z1) , large differential stress due to brittle rocks ; at greater depth A2 : high isotropic pressure (Plitho = r g Z2 ; Z2 > Z1) and low -differential- stress due to plastic rocks. Hatched : brittle – ductile transition.
Stress has also the dimension of a pressure, but it is « oriented » : it is maximum perpendicularly to s1 and minimum perpendicularly to s3 (s1 > s3). The value of the differential stress (s1 - s3), or stress hardly exceeds 100 MPa. Note that in everyday language, and also in many textbooks, stress means differential stress. Stress is represented as an ellipsoid whose long axis represents the maximum stress (s1) and the short axis, the minimum stress component (s3). This ellipsoid also increases with depth, i.e. the 3 axes increase in intensity, but the difference in length (intensity) between the long and the short axes does not exceed a certain value (100 MPa, as mentionned above).
The largest (differential) stress values are often close to the surface (because the rocks have a higher resistance to stress at low temperature that at high temperature !). Therefore, the ratio between the (differential) stress and the isotropic pressure decreases with inceasing depth. In other words, close to the surface, stress may be viewed as a rugby ball (whose axis is close to vertical), while at greater depth is looks like a large balloon whose shape is very close to spherical (with usually an horizontal long axis). At depth, the differential stress is the difference between the sphere and the quasi-spherical ellipsoid.
---------- Practical --------
It is difficult to escape from the writing of how stress, when applied to an element of surface (oriented by its normal), can be « decomposed » into a normal stress (normal contribution) and a tangential stress (tangential contribution). This is more than a simple vectorial decomposition since the surface in question is subjected to 3 principal stress (s1 ≥ s2 ≥ s3). Note that s1 , s2 and s3 are the 3 diagonal terms of the stress matrix s1j (second rank tensor) whose sum is equal to the 3-times the lithostatic pressure (Plitho = [s1 + s2 + s3] / 3 ).
Consider X, a point belonging to surface element SS’ (Figure).
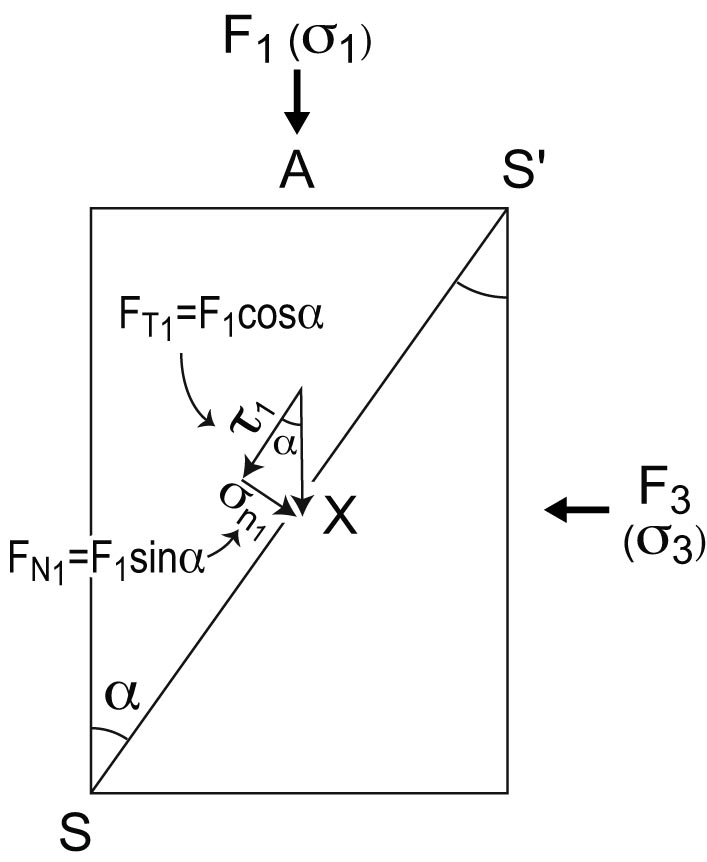
Decomposition, in the plane perpendicular to s2, of the force F1 = s1 / A which is applied to X (belonging to surface SS’) at an angle a. The same is done with F3(which makes an angle of 90° - a with SS’).
This surface element is oblique with respect to the force F1 that is applied to face A.
F1 resolves into two components, one which is normal to SS’ (Fn1 = F1 . sin a) and the other tangential to SS’ (FT1 = F1. cos a). One can deduce the values of sn1 and t1 : sn1 = Fn1 / SS’ (with SS’ = A / sin a) and t1 = FT1 / SS’.
A force F3 is also applied to face B, perpendicular to A, the components Fn3 and FT3 become sn3 = Fn3 / SS’ and t3 = FT3 / SS’ (with Fn3 = F3 cos a, FT1 = F3 sin a, and SS' = B / cos a).
The components (normal and tangential) of the stress which is applied to SS’ at X become :
snx = sn1 + sn3et tx= t1+ t3.
This leads to :
snx= F1 /A (sin2 a) + F3 /B (cos2 a) = s1sin2 a + s3cos2 a
tx= F1 /A (cosa . sina) - F3 /B (sin a . cos a), sign - meaning that the application of F3counteracts that of F1.
By using the « classical » trigonometric formulae (called double-angle formulae):
snx= s1(1- cos 2a) / 2 + s3(1+ cos 2a) / 2
or : snx= {[(s1+ s3) / 2] - [(s1- s3) / 2]} cos 2a
and : tx= [(s1- s3) / 2] sin 2a
Nota : the term (s1- s3) / 2 is called the stress deviator (often evoked among specialists in mechanics), its value is half of the differential stress.
Conformably with the presentation at the beginning of the paragraph, note that a stress tensor can be « decomposed » into an isotropic part (corresponding to the lithostatic pressure) and a deviatoric part :
s11 + s12 + s13 P/3 0 0 s11 - P/3 s12 s13
s12 + s22+ s23 = 0 P/3 0 + s12 s22 - P/3 s23
s13 + s23 + s33 0 0 P/3 s13 s23 s33 - P/3
-------------
Date: 2015-01-29; view: 1691
| <== previous page | | | next page ==> |
| Simple shear | | | The Mohr diagram |