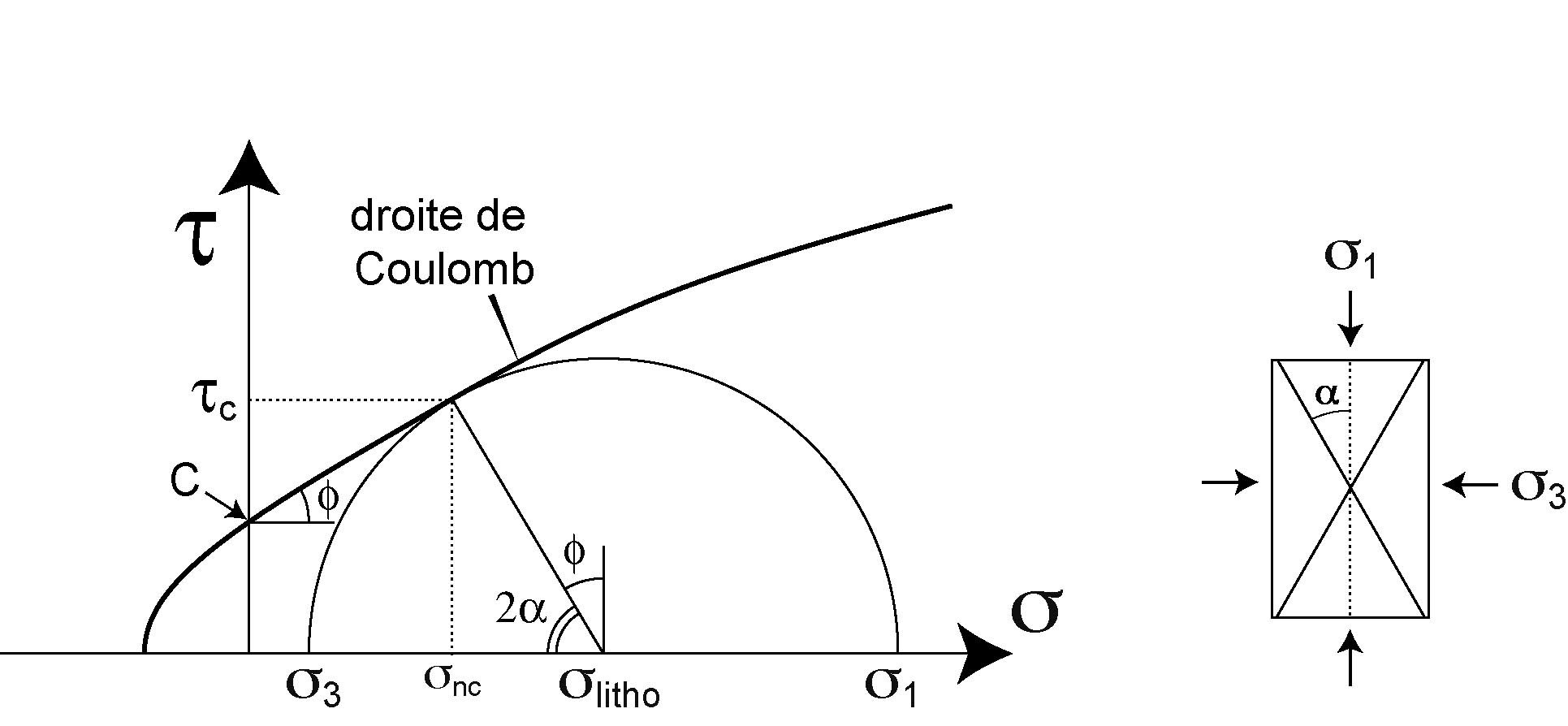
The Mohr diagram

These two last equations of s_nx and t_xare precisely the (polar) equations of the so-called Mohr circle in the (t , s) space. This diagram (Figure) is useful (and often used) to describe states of stress, and to understand the mechanics of rupture in rocks (« droite de Coulomb » : straight line representing the Coulomb’s law)

4. Stress-strain relationships

Among the infinity of relationships that may exist between stress and strain ….

(e_ij) tensor = (9x9) tensor x (s_1j) tensor

… let us examine simple (s, e) diagrams describing the elastic and the plastic behaviours (Figures)

- Elastic behaviour and elastic coefficients

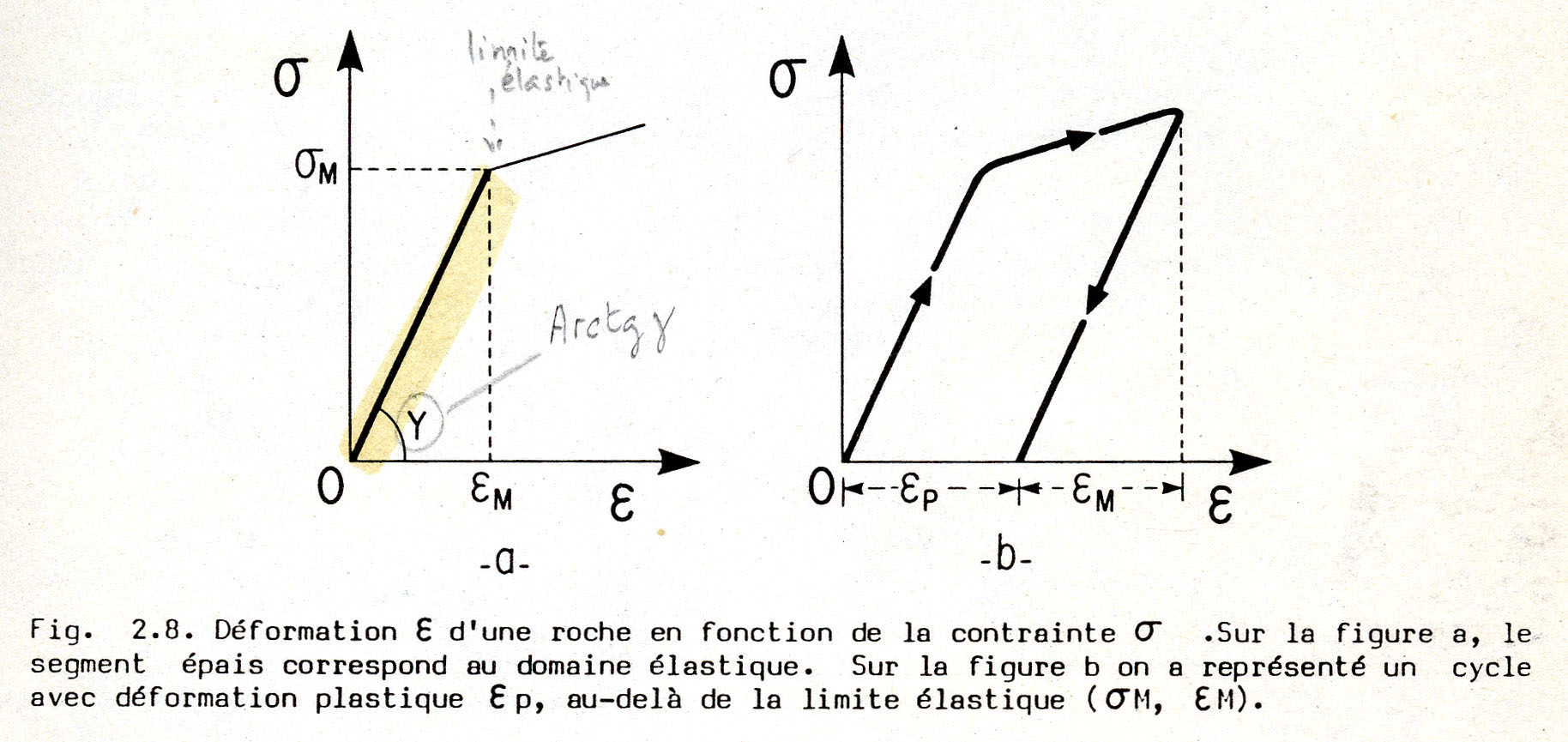
Figure : Linear dependence of deformation e with respect to stress s. In (a) the segment in bold represents the elastic part (reversible) of the deformation up to the yield stress s_M, e_M being the elastic limit of the material. (b) Above the yield stress, plastic (or permanent) deformation is observed, giving e_P. Note that e_M is usually very small, on the order of a few per mil (‰) in silicates, exceptionally much larger in is purely elastic rubber.

This diagram gives a basic description of elasticity which depends only on the elastic modulus, or Young’s modulus E :

s = E e

In case of isotropic (usual) materials, in-between the stress tensor (s_ij : 3x3 : rank 2 tensor) and the strain tensor (e_ij : 3x3 : rank 2 tensor), there is the elastic tensor which is a 9x9 tensor (C_ijkl : rank 4 tensor) containing 81 elastic coefficients (scalar elements). Due to the symmety of the tensor (and to other properties), the number of independent coefficients is much reduced.

In practice, a limited number of elastic coefficients are commonly used inddition to E. The main one is the Poisson’s coefficient (n) that characterizes the retraction of a material (along x or y) perpendicularly to an applied effort (along z):

e_x/e_z = e_y/e_z = - n (value in-between – 1 and 0.5)

Most hard (normal) materials (rocks …) have Poissons’s coefficients around 0,3

The Poisson’s coefficient (or Poisson’s ratio) is commonly invoked by sismologists since it expresses the ability of rocks to behave more or less plastically under compression waves (P waves).

E and n combine into the elasticity module : K = E / 3 [1-2n)], such that K = E

for n = 0,33 (« normal » materials), and K ॠ(incompressibility) for n = 0.5 (pure rubber).

Finally, the shear modulus G is often used when elastic shear is concerned ; it relationship with E and n is as follows : E = 2G (1 + n)

- Plastic behaviours

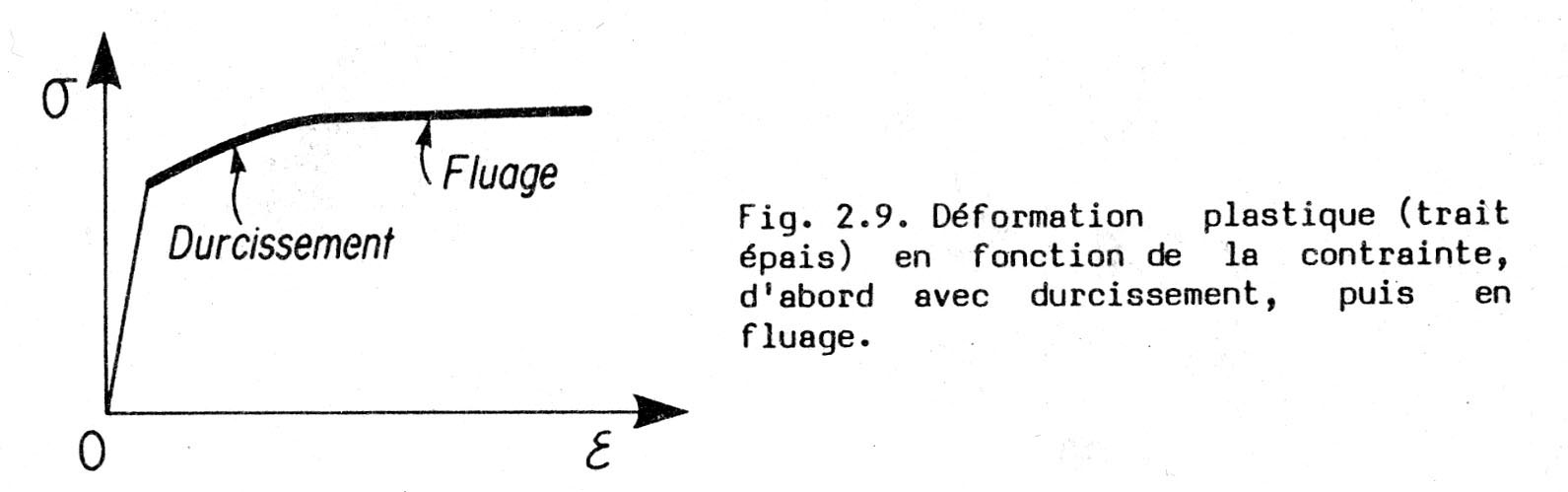
According to the slope of the (s, e) curve, creep (fluage in French) is distinguished from hardening (durcissement in French), and from weakening, softening (not represented, negative slope). Note that e may have very large values …

Have you experienced hardening : in metals ? during cooking preparation ?

- In metals : the blacksmith forging horseshoes … hardens them by cooling them very rapidly in cold water.

- In cooking, when you prepare mayonaise, you harden the mayonaise by beating it.

Have you experienced softening : in cooking ? … when your mayonaise progressively turns into a liquid ? in materials in general, when you increase the temperature, for example.

In fact, a (s, e) description for plastic deformation, which corresponds to large deformation and makes it very close to flow in fluid mechanics, is far from being sufficient. Instead, in rock mechanics, the pertinent relationship is between s and e’ (de/dt).

Most flaw laws in plastic deformation of rocks have the following relationship between s and e^’:

e^’ =  . s ⁿ [exp (-Q/RT)]

… the value of the stress exponent (n) is around 3 if the deformation in the crystals (hence in the whole rock) is performed through the mobility of dislocations. It may be much higher than 3 (n >> 3) in case of the so-called « superplasticity » (close to a « ball-bearing » mechanism). Note that n = 1 in case of a newtonian flow which characterizes (ideal) fluids.

… the term [exp (-Q/RT)] is the diffusive term which expresses the role of temperature. The exponential function indicates the extreme sensitivity of the strain rate (e^’) to temperature. Q is called the activation energy depends on the nature of the crystalline nature of the material.

5. Stress magnitudes on Earth and in situ stress determination

The intensity of the (differential) stress is maximum close to the surface where rocks are « hard », hence are able to undergo large pressures : stress magnitudes up to 1 kb (100 MPa) and more are invoked. Their measurement is not easy to realize (see « in situ stress determination »).

As soon as rocks become soft, plastic, due to temperature increase, their ability to carry stress is reduced, down to a few bars in the mantle, since they release stress through deformation.

Stress measurements can be performed close to the surface through different techniques (see lesson n°5)

Date: 2015-01-29; view: 2529