Simple shear

The simplest deformation, and also the most common on Earth, is simple shear. Simple shear is a homogeneous, and « planar » (2D) deformation : the Y axis is invarant ; « all the deformation takes place in the XZ plane ».

Simple shear is often represented as the deformation of a circle into an ellipse (Figure), or of a square into a lozange, in which each material point is displaced parallel to the shear direction. Simple shear is characterized by the shear angle (q) or shear stress g = tg (q).

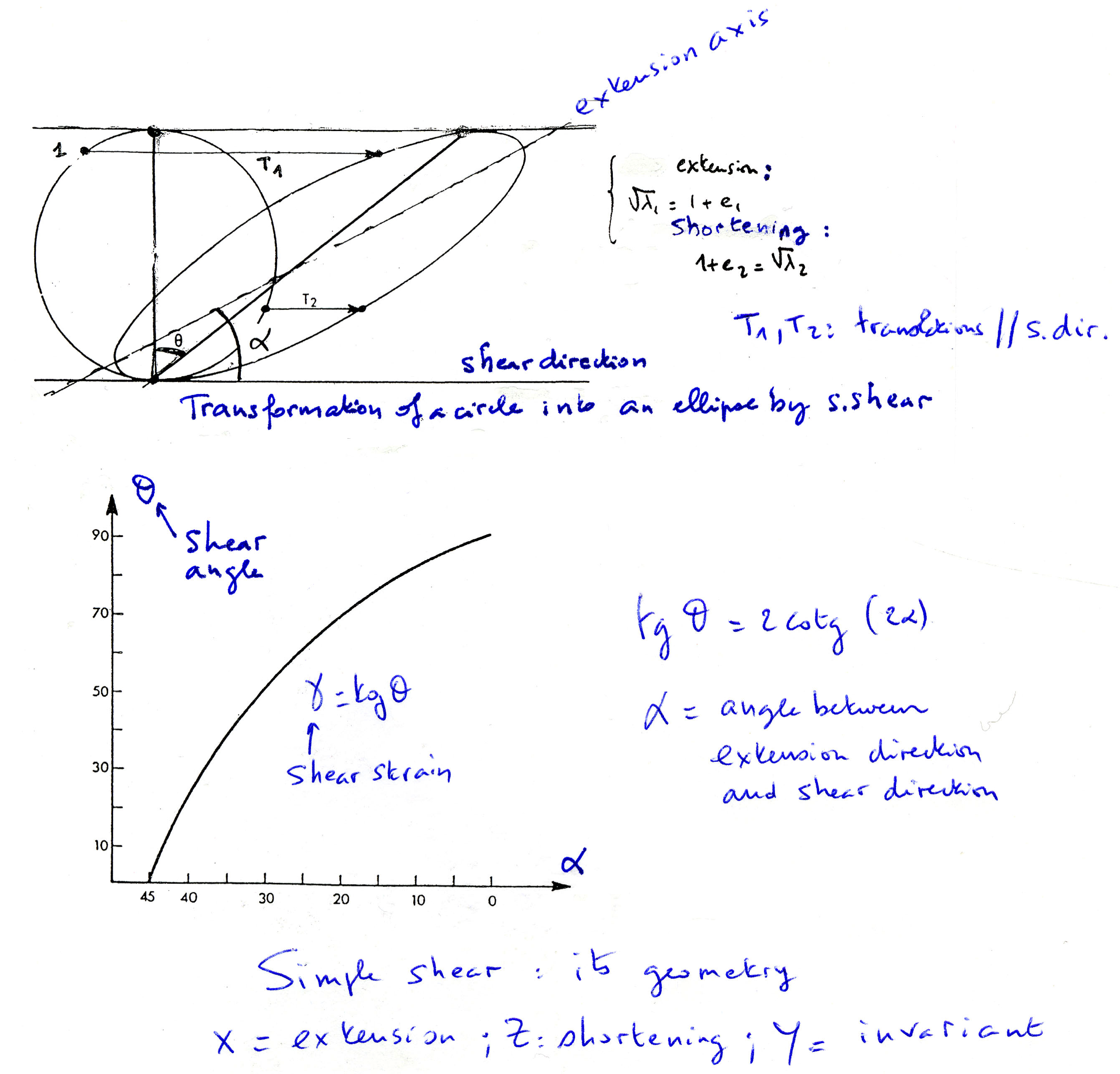
Simple shear is a non-coaxial deformation : X (the extension axis) is continuously rotating with increasing q. The angle (a) between X and the shear direction (horizontal in the figure) decreases continuously down to 0 with increasing q.

The extension direction at q = 0°+ (very beginning of deformation) makes an angle of 45° to the shear direction. At q = 90° (infinite deformation), every material point is parallel to the shear direction. Note that, as soon as the Y axis varies (elongation, contraction), the deformation is no more a simple shear (which is planar by definition). This deformation it said as having a non-coaxial component (vorticity number ¹ 1, see hereunder).

Date: 2015-01-29; view: 1582