Deformation and the structural framework

In a broad sense, deformation can be defined as a change in the relative positions (displacement) of material points of a given body (rock) due to the action of a stress (force applied on the surface of the body).

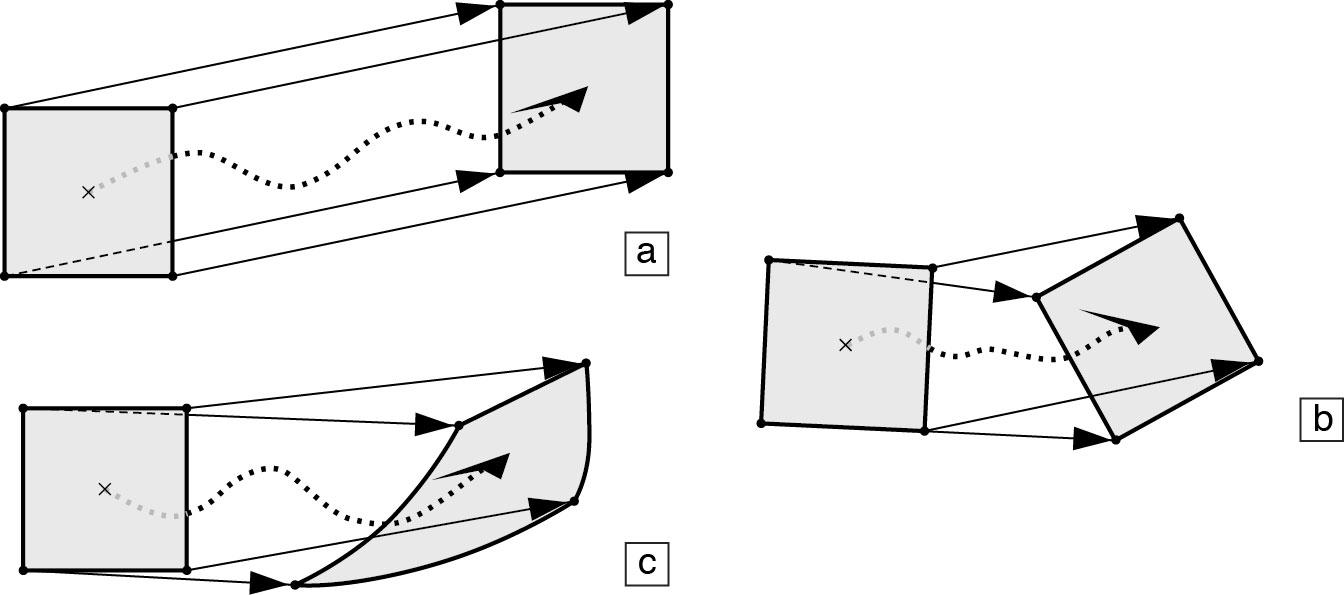
Streakly speaking, displacement, or deformation sensu lato is a translation (a) + a bulk rotation (b) + a distorsion (c) or deformation sensus stricto, also called « internal deformation ». Note that (c) is a heterogenous deformation.

Note that a deformation (s.str.) can be homogeneous (a : every material point is deformed in the same way), heterogeneous but continuous (b) or discontinuous (c).

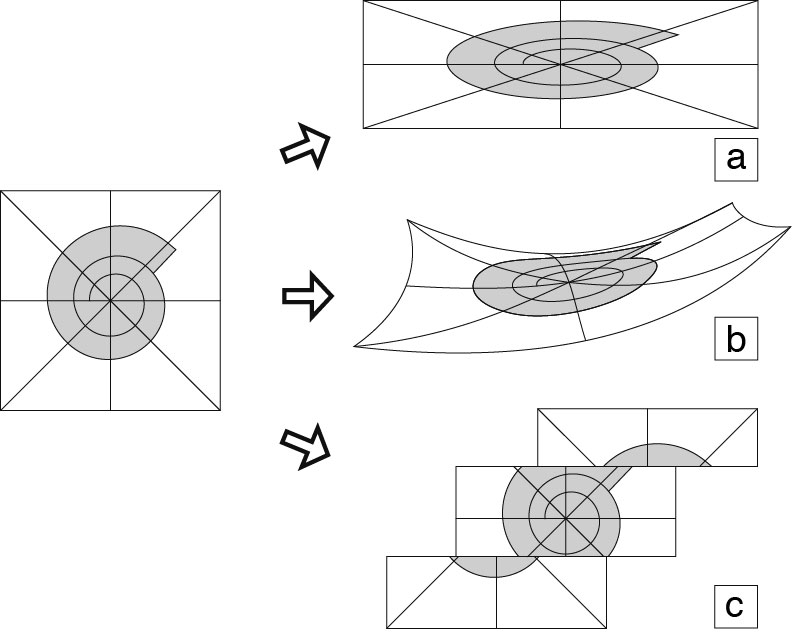
In practice, homogeneity of deformation is scale-dependent. A homogeneous deformation at a given scale (a) may not necessarily be homogeneous at a larger scale (b : Figure) :

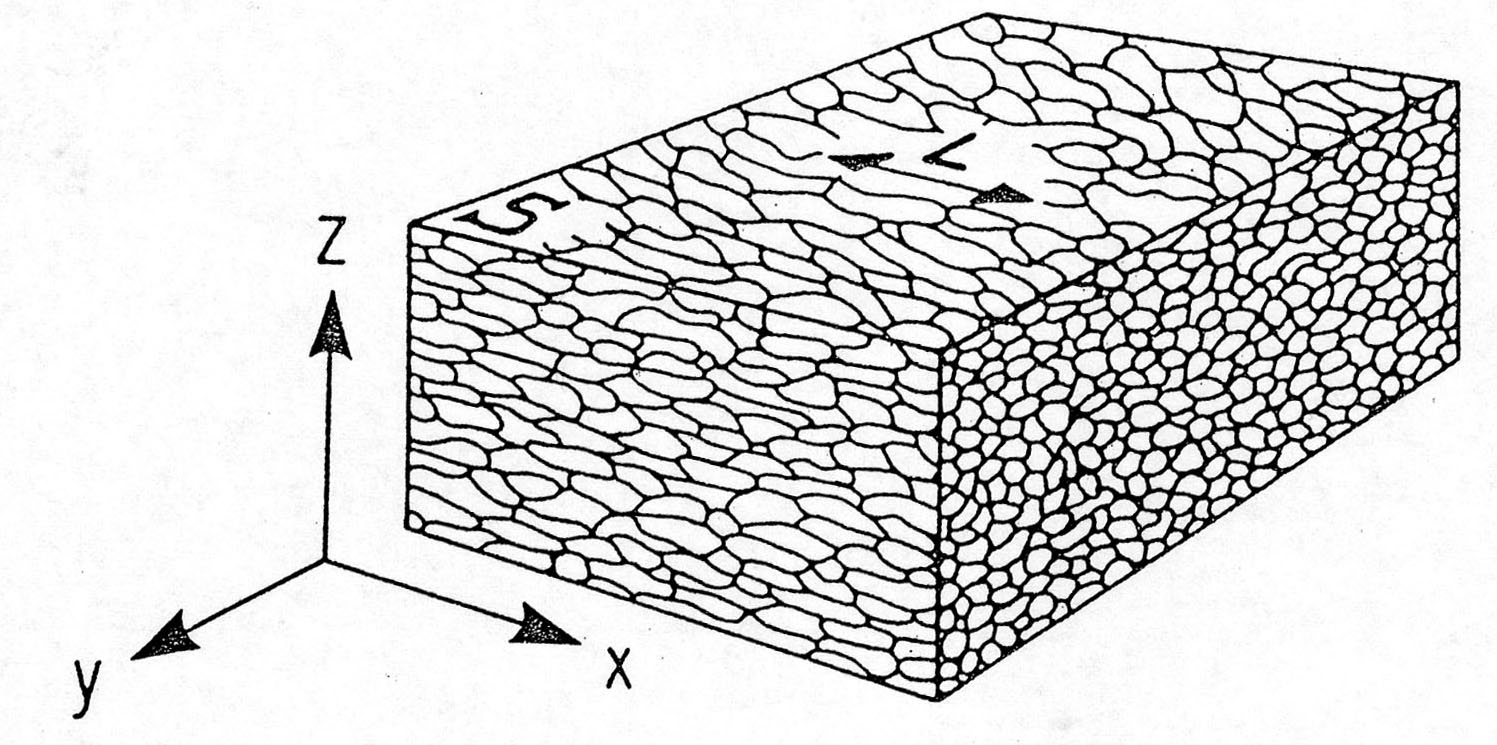
By definition, deformed objects, rocks, are stretched along X (lineation) and flattened (foliated) perpendicularly to Z. The Y axis is perpendicular to X and Z. X ≥ Y ≥ Z define the structural framework.

In geology, in rock mechanics … a material is often analysed as homogeneously (and therefore continuously) deformed, at least at a small scale (km, m, mm …).

Date: 2015-01-29; view: 2213