
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Decoding problems
A codeword t is selected from a linear (N,K) code C, and it is transmitted over a noisy channel; the received signal is y. Here we will assume that the channel is a memoryless channel such as a Gaussian channel. Given an assumed channel model P(y | t), there are two decoding problems.
The codeword decoding problem is the task of inferring which codeword t was transmitted given the received signal.
The bitwise decoding problem is the task of inferring for each transmitted bit tn how likely it is that that bit was a one rather than a zero.
As a concrete example, take the (7; 4) Hamming code. We discussed the codeword decoding problem for that code, assuming a binary symmetric channel. We didn't discuss the bitwise decoding problem and we didn't discuss how to handle more general channel models such as a Gaussian channel.
Solving the codeword decoding problem
By Bayes' theorem, the posterior probability of the codeword t is
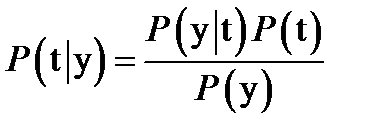
Decoding with the sum–product algorithm
We aim, given the observed checks, to compute the marginal posterior probabilities P(xn =1 | z,H) for each n. It is hard to compute these exactly because the graph contains many cycles. However, it is interesting to implement the decoding algorithm that would be appropriate if there were no cycles, on the assumption that the errors introduced might be relatively small. Cost. In a brute-force approach, the time to create the generator matrix scales as N3, where N is the block size. The encoding time scales as N2, but encoding involves only binary arithmetic, so for the block lengths studied here it takes considerably less time than the simulation of the Gaussian channel.
Decoding involves approximately 6Nj floating-point multiplies per iteration, so the total number of operations per decoded bit (assuming 20 iterations) is about 120t/R, independent of blocklength.
The encoding complexity can be reduced by clever encoding tricks.
The decoding complexity can be reduced, with only a small loss in performance, by passing low-precision messages in place of real numbers.
Date: 2015-01-29; view: 1170
| <== previous page | | | next page ==> |
| Convexity and Jensen's inequality | | | Definition of the typical set |