
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Definition of the typical set
Let us define typicality for an arbitrary ensemble X with alphabet χ. Our definition of a typical string will involve the string's probability. A long string of N symbols will usually contain about p1N occurrences of the first symbol, p2N occurrences of the second, etc. Hence the probability of this string is roughly
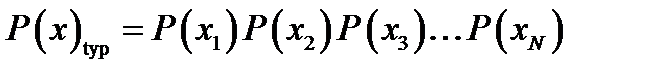
so that the information content of a typical string is
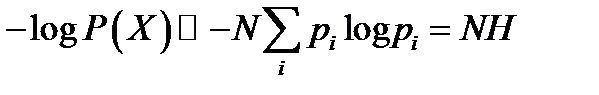 Why did we introduce the typical set?
Why did we introduce the typical set?
The best choice of subset for block compression is (by definition) Sδ, not a typical set. So why did we bother introducing the typical set? The answer is, we can count the typical set. We know that all its elements have “almost identical” probability (2-NH), and we know the whole set has probability almost 1, so the typical set must have roughly 2NH elements. Without the help of the typical set (which is very similar to Sδ) it would have been hard to count how many elements there are in Sδ.
Density evolution
density evolution
is used in
I
analyzing channel codes
I
analyzing solution space of XORSAT
I
analyzing a message-passing algorithm for crowdsourcing
I
etc

Describe the disadvantages of the Huffman code.

The Huffman algorithm produces an optimal symbol code for an ensemble, but this is not the end of the story. Both the word “ensemble” and the phrase “symbol code” need careful attention.
Changing ensemble
If we wish to communicate a sequence of outcomes from one unchanging ensemble, then a Huffman code may be convenient. But often the appropriate ensemble changes. If for example we are compressing text, then the symbol frequencies will vary with context: in English the letter u is much more probable after a q than after an e. And furthermore, our knowledge of these context-dependent symbol frequencies will also change as we learn the statistical properties of the text source.
The extra bit
An equally serious problem with Huffman codes is the innocuous-looking extra bit relative to the ideal average length of H(X) – a Huffman code achieves a length that satisfies H(X) ≤ L(C,X) < H(X) + 1
A Huffman code thus incurs an overhead of between 0 and 1 bits per symbol.
Beyond symbol codes
Huffman codes, therefore, although widely trumpeted as “optimal”, have many defects for practical purposes. They are optimal symbol codes, but for practical purposes we don't want a symbol code. The defects of Huffman codes are rectified by arithmetic coding, which dispenses with the restriction that each symbol must translate into an integer number of bits.
Describe the Lempel–Ziv coding.
The Lempel-Ziv algorithms, which are widely used for data compression (e.g., the compress and gzip commands), are different in philosophy to arithmetic coding. There is no separation between modelling and coding, and no opportunity for explicit modelling.
Example Encode the string 000000000000100000000000 using the basic Lempel-Ziv algorithm described above.
The encoding is 010100110010110001100, which comes from the parsing
0, 00, 000, 0000, 001, 00000, 000000
which is encoded thus:
(, 0), (1, 0), (10, 0), (11, 0), (010, 1), (100, 0), (110, 0)
Decode the string 00101011101100100100011010101000011 that was encoded using the basic Lempel-Ziv algorithm.
The decoding is 0100001000100010101000001
Describe the main research method signals.
Research in common parlance refers to a search for knowledge. Once can also define research as
a scientific and systematic search for pertinent information on a specific topic. In fact, research is an
art of scientific investigation.
Describe the Noisy-Channel coding theorem (extended).
The Noisy-Channel Coding Theorem (extended)
The theorem has three parts, two positive and one negative.
1. For every discrete memoryless channel, the channel capacity
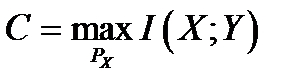
has the following property. For any ε > 0 and R < C, for large enough N, there exists a code of length N and rate ≥ R and a decoding algorithm, such that the maximal probability of block error is < ε.
2. If a probability of bit error pb is acceptable, rates up to R(pb) are achievable, where
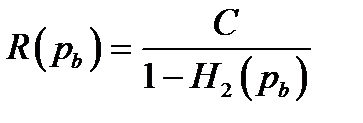
3. For any pb, rates greater than R(pb) are not achievable.
Describe the types of information systems and their development.
1. knowledge area (biologic, industry, financial, etc)
2. physical nature (acoustic, visual, gustatory)
3. Structural-measurement properties.
Parametric information – contains numerical evaluation of different properties.
| Information types | Key | Information representation form | ||
| Topologic | Abstract | Linguistic | ||
| event value function complex ................ field | Ô0 Ô1 Ô2 Ô3 ......... Ôn | point line surface volume .............. dimension | opinion idea image system ............. universe | sign character word sentence ............... fund |
Designing the degree distribution
The probability distribution ρ(d) of the degree is a critical part of the design: occasional encoded packets must have high degree (i.e., d similar to K) in order to ensure that there are not some source packets that are connected to no-one. , to avoid redundancy, we'd like the received graph to have the property that just one check node has degree one at each iteration. At each iteration, when this check node is processed, the degrees in the graph are reduced in such a way that one new degree-one check node appears. In expectation, this ideal behaviour is achieved by the ideal soliton distribution,

The expected degree under this distribution is roughly lnK.
Date: 2015-01-29; view: 1863
| <== previous page | | | next page ==> |
| Decoding problems | | | Digital Fountain Codes |