
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Convexity and Jensen's inequality
A large part of information theory consists in finding bounds on certain performance measures. The analytical idea behind a bound is to substitute a complicated expression for something simpler but not exactly equal, known to be either greater or smaller than the thing it replaces. This gives rise to simpler statements (and hence gain some insight), but usually at the expense of precision.
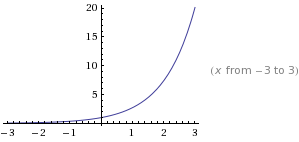
A function f(x) is said to be convex over an interval (a,b) if for every 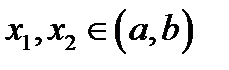 and
and 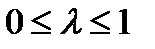 ,
,
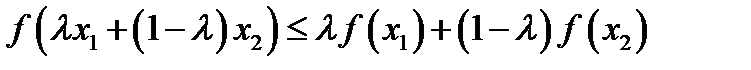
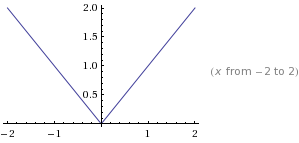
A function is strictly convex if equality holds only if 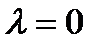 or
or 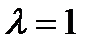 .
.
Convex 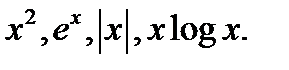
Concave: 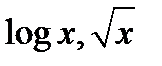
Theorem 8 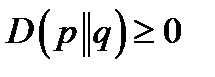 , with equality if and only if p(x) = q(x) for all x.
, with equality if and only if p(x) = q(x) for all x.
Proof
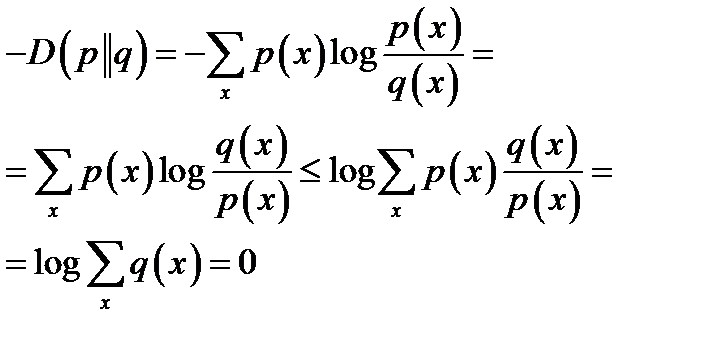
Data compression
The preceding examples justify the idea that the Shannon information content of an outcome is a natural measure of its information content. Improbable outcomes do convey more information than probable outcomes. We now discuss the information content of a source by considering how many bits are needed to describe the outcome of an experiment. If we can show that we can compress data from a particular source into a file of L bits per source symbol and recover the data reliably, then we will say that the average information content of that source is at most L bits per symbol.
Some simple data compression methods that define measures of information content
Example
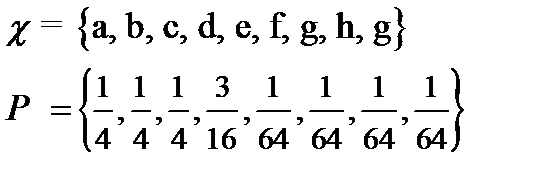
The raw bit content of this ensemble is 3 bits, corresponding to 8 binary names. But notice that 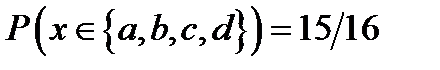 . So if we are willing to run a risk of
. So if we are willing to run a risk of 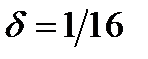 of not having a name for x, then we can get by with four names – half as many names as are needed if every x has a name.
of not having a name for x, then we can get by with four names – half as many names as are needed if every x has a name.

Decoding convolutional codes
The receiver receives a bit stream, and wishes to infer the state sequence and thence the source stream. The posterior probability of each bit can be found by the sum–product algorithm (also known as the forward–backward or BCJR algorithm). The most probable state sequence can be found using the min–sum algorithm (also known as the Viterbi algorithm).
Date: 2015-01-29; view: 1498
| <== previous page | | | next page ==> |
| Coding and Modulation in data transmission systems. | | | Decoding problems |