Coding and Modulation in data transmission systems.

Coding and modulation provide the means of mapping information into waveforms such that the receiver (with an appropriate demodulator and decoder) can recover the information in a reliable manner. The simplest model for a communication system is that of an additive white Gaussian noise (AWGN) system. In this model a user transmits information by sending one of M possible waveforms in a given time, period T, with a given amount of energy. The rate of communication, R, in bits per second is log₂(M)/T. The signal occupies a given bandwidth W Hz. The normalized rate of communications is R/W measured in bits/second/Hz.

Data transmission, digital transmission, or digital communications is the physical transfer of data (a digital bit stream) over a point-to-point or point-to-multipoint communication channel. Examples of such channels are copper wires, optical fibres, wireless communication channels, and storage media. The data are represented as an electromagnetic signal, such as an electrical voltage, radiowave, microwave, or infrared signal.

Collision resolution

We will study two ways of resolving collisions: appending in the table, and storing elsewhere.

Appending in table

When encoding, if a collision occurs, we continue down the hash table and write the value of s into the next available location in memory that currently contains a zero. If we reach the bottom of the table before encountering a zero, we continue from the top.

For this method, it is essential that the table be substantially bigger in size than S. If 2^M < S then the encoding rule will become stuck with nowhere to put the last strings.

Storing elsewhere

As an example, we could store in location h in the hash table a pointer (which must be distinguishable from a valid record number s) to a “bucket” where all the strings that have hash code h are stored in a sorted list. The encoder sorts the strings in each bucket alphabetically as the hash table and buckets are created.

This method of storing the strings in buckets allows the option of making the hash table quite small, which may have practical benefit

Conditional entropy and its properties.

In information theory, the conditional entropy (or equivocation) quantifies the amount of information needed to describe the outcome of a random variable 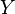given that the value of another random variable 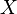is known. Here, information is measured in bits, nats, or bans. The entropy of 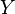conditioned on 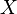is written as .

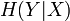Given discrete random variable 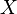with support 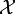and 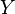with support , the conditional entropy of 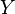given 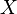is defined as:

Date: 2015-01-29; view: 857