Example: compressing the tosses of a bent coin

Capacity of Gaussian channel

Until now we have measured the joint, marginal, and conditional entropy of discrete variables only. In order to define the information conveyed by continuous variables, there are two issues we must address – the infinite length of the real line, and the infinite precision of real numbers.

Additive white Gaussian noise (AWGN) is a channel model in which the only impairment to communication is a linear addition of wideband or white noise with a constant spectral density (expressed as watts per hertz of bandwidth) and a Gaussian distribution of amplitude.

The AWGN channel is represented by a series of outputs 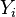at discrete time event index . 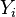is the sum of the input 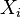and noise, 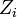, where 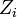is independent and identically distributed and drawn from a zero-mean normal distribution with variance (the noise). The 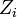are further assumed to not be correlated with the .

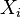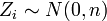
The capacity of the channel is infinite unless the noise n is nonzero, and the 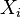are sufficiently constrained. The most common constraint on the input is the so-called "power" constraint, requiring that for a codeword 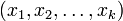transmitted through the channel, we have:

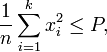
where 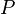represents the maximum channel power. Therefore, the channel capacity for the power-constrained channel is given by:

Where 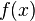is the distribution of 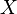. Expand 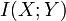, writing it in terms of the differential entropy:

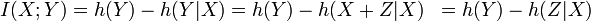
But 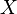and 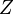are independent, therefore:

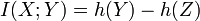
Codes and trellises

Linear (N,K) codes could be represented in terms of their generator matrices and their parity-check matrices. In the case of a systematic block code, the first K transmitted bits in each block of size N are the source bits, and the remaining M = N – K bits are the parity-check bits. This means that the generator matrix of the code can be written

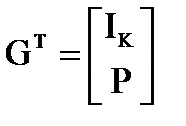
and the parity-check matrix can be written

where P is an M × K matrix.

Here we will study another representation of a linear code called a trellis. The codes that these trellises represent will not in general be systematic codes, but they can be mapped onto systematic codes if desired by a reordering of the bits in a block.

A trellis is a graph consisting of nodes (also known as states or vertices) and edges. The nodes are grouped into vertical slices called times, and the times are ordered such that each edge connects a node in one time to a node in a neighbouring time.

Example:

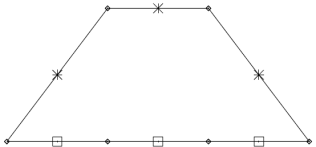
(a) Repetition code R3

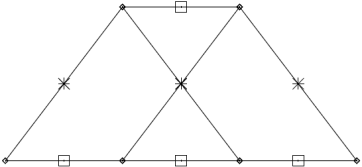
(b) Simple parity code P3

Date: 2015-01-29; view: 1010