Calculating the pH of an Aqueous Solution of the Salt of a Weak Acid and weak base?

Calculating the pH of an Aqueous Solution of the Salt of a Weak Acid

Calculating the pH of an Aqueous Solution of the Salt of a Weak Base

What is Primary standard and secondary standard and their properties, titrimetry methods? What is titrant and analyte, Indicator and indicator’s properties, equivalence point or end point?

Standard solution :

A solution of precisely known concentration.

Primary standard :

An ultra-pure (99.9% purity) compound that serves as the reference material for a titrimetric method of analysis.

Secondary standard :

A compound whose purity has been established by chemical analysis and that serves as the reference material for a titrimetric method of analysis

Standardization :

a process in which the concentration of a solution is determined by using the solution to titrate a known amount of another reagent.

Primary standard :

Our titrant solutions must be of known composition and concentration

ideally, we would like to start with a primary standard material.

Primary standard

A high purity compound used to prepare our standard solution or to standardize the solution with.

Desired properties if a primary standard High purity

Stable in are and solution

Not hydroscopic Inexpensive

Large formula weight

Soluble in our solvent

Reacts rapidly and stoichiometrically with our solvent

Few materials have all of these properties

Primary standard

A material that is stable in a bottle may not remain that way in solution.

A primary standard solution should:

Have long term stability in your solvent.

React rapidly with your analyte React completely with your analyte

Be selective for your analyte

The last requirement is often based on the procedure used.

The secondary standard

Suitable primary standards are not always available for a given titration.

You must often rely on a second material for your titrant. It should always be standardized using a primary standard.

This second material is then considered a secondary standard.

Titrant :

The substance that quantitatively reacts with the analyte in a titration . The titrant is usually a standard solution added carefully to the analyte until the reaction is complete. The amount of analyte is calculated from the volume of titrant required for complete reaction.

Analyte is an unknown substance.

Indicator :

An indicator is used to find the end-point of the titration. The end-point is the point where the indicator changes colour. This may not be at the equivalence point

A substance that undergoes an sharp, easily observable physical change when conditions in its solutions change. See, for example, acid-base indicator and redox indicator .

For an acid base titration the equivalence point is the point where neutralisation occurs.

Indicators must have the following properties :

a) the color change must be sharp. i.e. the indicator must change colour with the addition of one drop of solution from the burette.

b) change colour as close to the equivalence point as possible

c) Give a distinct colour change.

Equivalence point : in a titration occurs when the requirements of the balanced equation for reaction are exactly satisfied.

End point : the point in a titration when a physical change occurs that is associated with the condition of chemical equivalence.

The point in a titration at which equivalent amounts of titrant is the exact amount necessary for stoichiometric reaction with the analyte.

The point where sufficient titrant has been added to be stoichiometrically equivalent to the amount of analyte.

Just enough titrant has been added to react with all of our analyte

Acid–Base Titrations curve? titrating strong acids and strong bases and their curve?

Before 1800, most acid–base titrations used H₂SO₄, HCl, or HNO₃ as acidic titrants, and K₂CO₃ or Na₂CO₃ as basic titrants. A titration’s end point was determined using litmus as an indicator, which is red in acidic solutions and blue in basic solutions, or by the cessation of CO₂ effervescence when neutralizing CO₃^2-. Early examples of acid–base titrimetry include determining the acidity or alkalinity of solutions, and determining the purity of carbonates and alkaline earth oxides.

Acid–Base Titration Curves

In the overview to this chapter we noted that a titration’s end point should coincide with its equivalence point. To understand the relationship between an acid–base titration’s end point and its equivalence point we must know how the pH changes during a titration. In this section we will learn how to calculate a titration curve using the equilibrium calculations. We also will learn how to quickly sketch a good approximation of any acid–base titration curve using a limited number of simple

calculations.

TITRATING STRONG ACIDS AND STRONG BASES

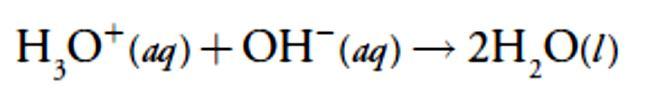For our first titration curve, let’s consider the titration of 50.0 mL of 0.100M HCl using a titrant of 0.200 M NaOH. When a strong base and a strong acid react the only reaction of importance is

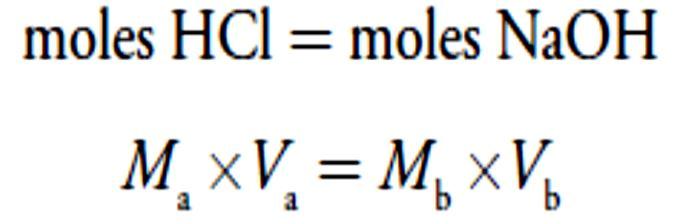The first task in constructing the titration curve is to calculate the volume of NaOH needed to reach the equivalence point, Veq. At the equivalence point we know from reaction that

where the subscript ‘a’ indicates the acid, HCl, and the subscript ‘b’ indicates the base, NaOH. The volume of NaOH needed to reach the equivalence point is

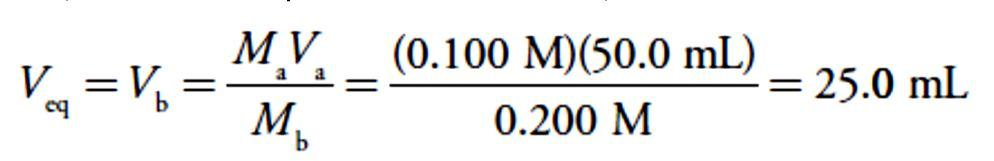
Before the equivalence point, HCl is present in excess and the pH is determined by the concentration of unreacted HCl. At the start of the titration the solution is 0.100 M in HCl, which, because HCl is a strong acid, means that the pH is

After adding 10.0 mL of NaOH the concentration of excess HCl is

and the pH increases to 1.30.

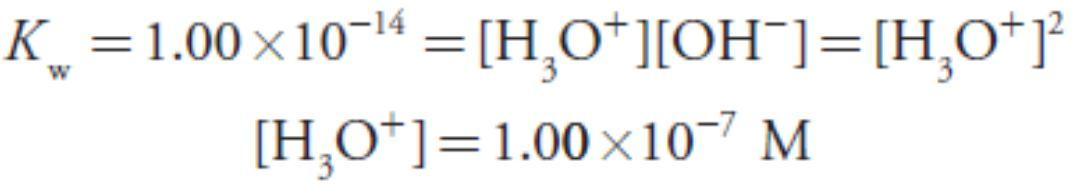At the equivalence point the moles of HCl and the moles of NaOH are equal. Since neither the acid nor the base is in excess, the pH is determined by the dissociation of water.

Thus, the pH at the equivalence point is 7.00.

For volumes of NaOH greater than the equivalence point, the pH is determined by the concentration of excess OH^–. For example, after adding 30.0 mL of titrant the concentration of OH– is

To find the concentration of H₃O⁺ we use the Kw expression

giving a pH of 12.10.

Titrating a weak acid with a strong base and their curve? multiprotic acids or bases, and mixtures of acids or bases and their curve?

TITRATING A WEAK ACID WITH A STRONG BASE

For this example, let’s consider the titration of 50.0 mL of 0.100 M acetic acid, CH3COOH, with 0.200 M NaOH. Again, we start by calculating the volume of NaOH needed to reach the equivalence point; thus

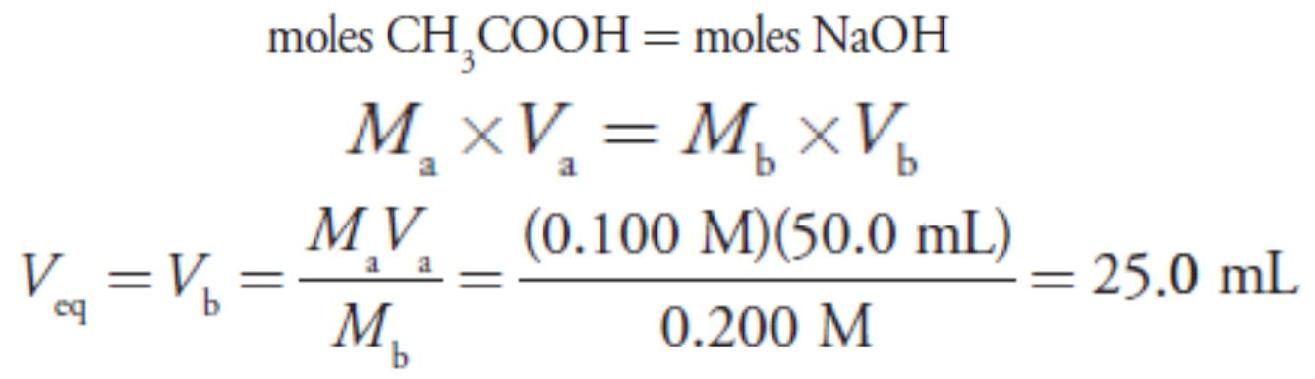
Before adding NaOH the pH is that for a solution of 0.100 M acetic acid. Because acetic acid is a weak acid, we calculate the pH.

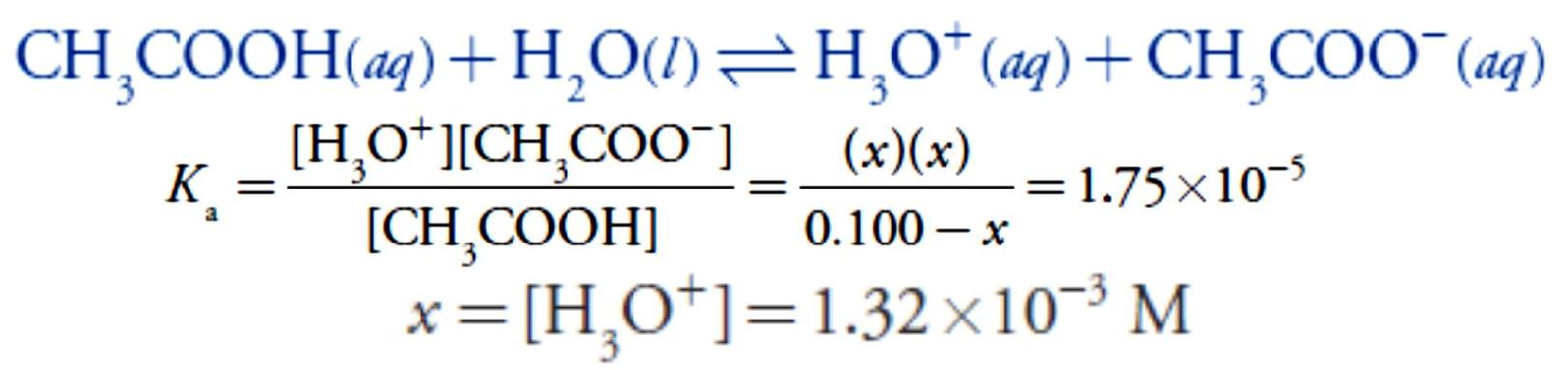
At the beginning of the titration the pH is 2.88.

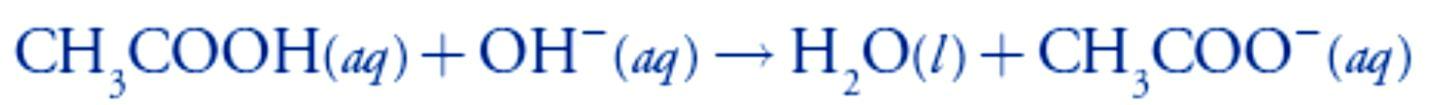Adding NaOH converts a portion of the acetic acid to its conjugate base, CH3COO^–.

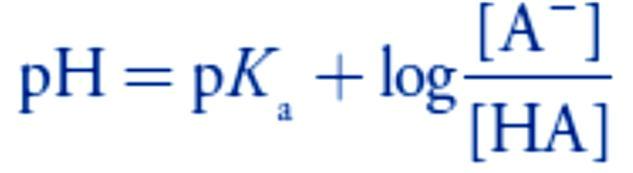Any solution containing comparable amounts of a weak acid, HA, and its conjugate weak base, A–, is a buffer. As we learned in lecture 4, we can calculate the pH of a buffer.

Before the equivalence point the concentration of unreacted acetic acid is

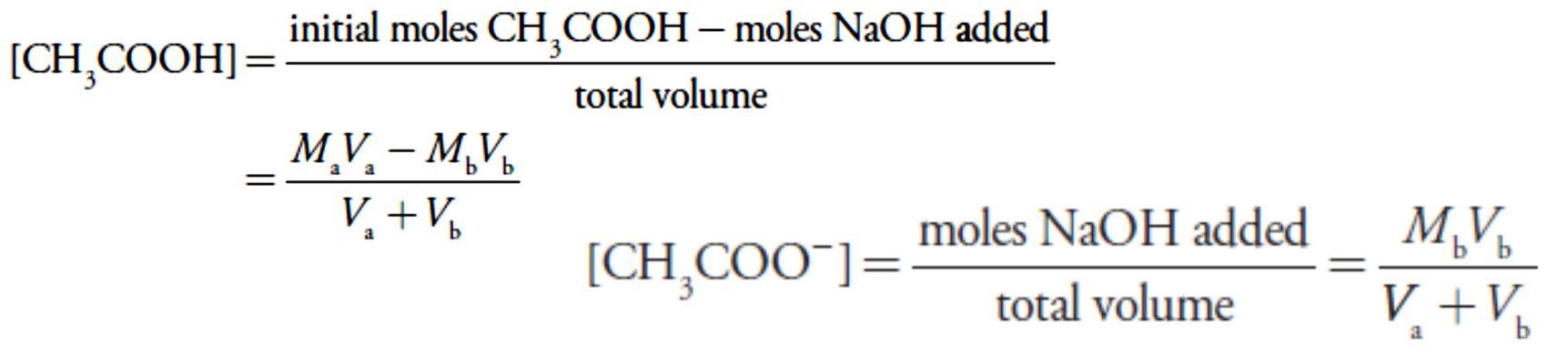
and the concentration

of acetate is

For example, after adding 10.0 mL of NaOH the concentrations of CH3COOH and CH3COO^– are

which gives us a pH of

At the equivalence point the moles of acetic acid initially present and the moles of NaOH added are identical. Because their reaction effectively proceeds to completion, the predominate ion in solution is CH3COO^–, which is a weak base. To calculate the pH we first determine the concentration of CH3COO^–

Next, we calculate the pH of the weak base as shown earlier in lecture 6.

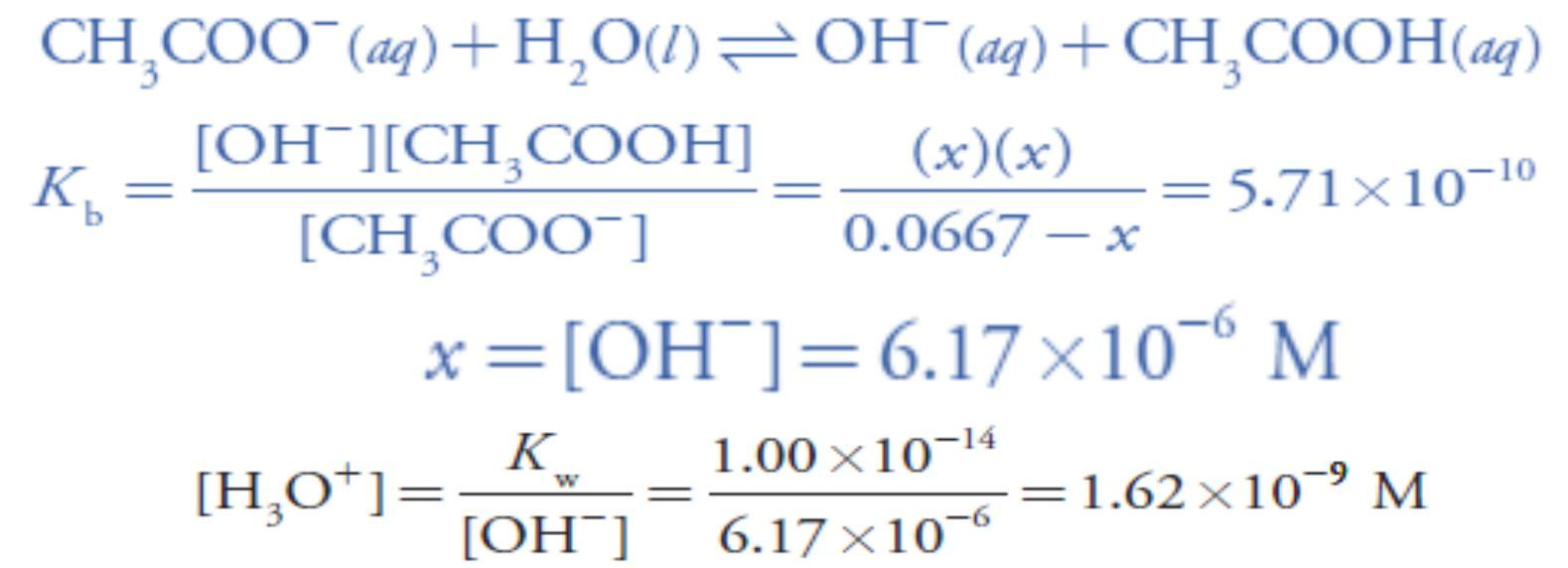
The pH at the equivalence point is 8.79.

After the equivalence point, the titrant is in excess and the titration mixture is a dilute solution of NaOH. We can calculate the pH using the same strategy as in the titration of a strong acid with a strong base. For example, after adding 30.0 mL of NaOH the concentration of OH^– is

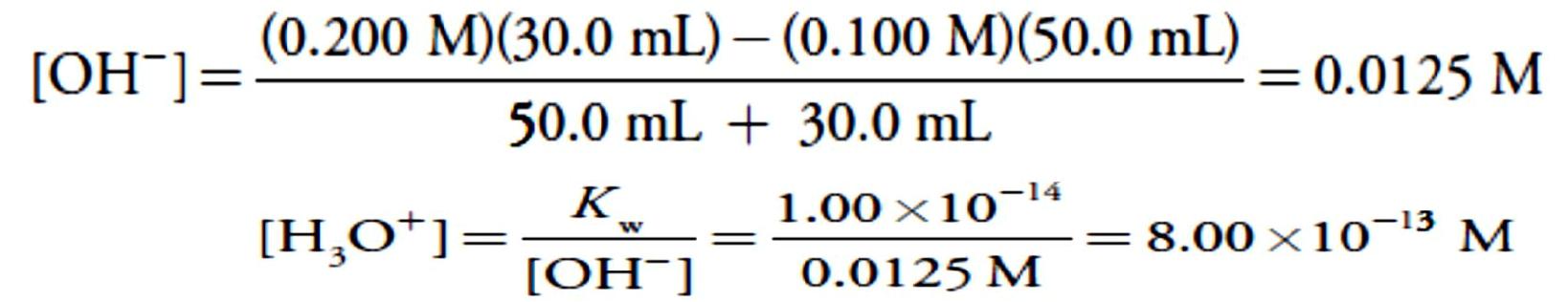
giving a pH of 12.10. Table 2 and Figure 3 show additional results for this titration. You can use this same approach to calculate the titration curve for the titration of a weak base with a strong acid, except the initial pH is determined by the weak base, the pH at the equivalence point by its conjugate weak acid, and the pH after the equivalence point by excess strong acid.

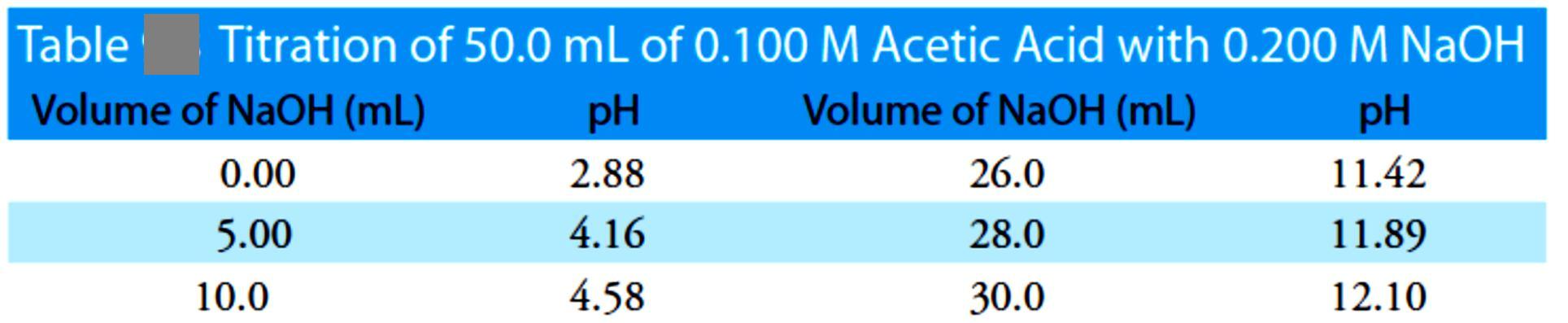2

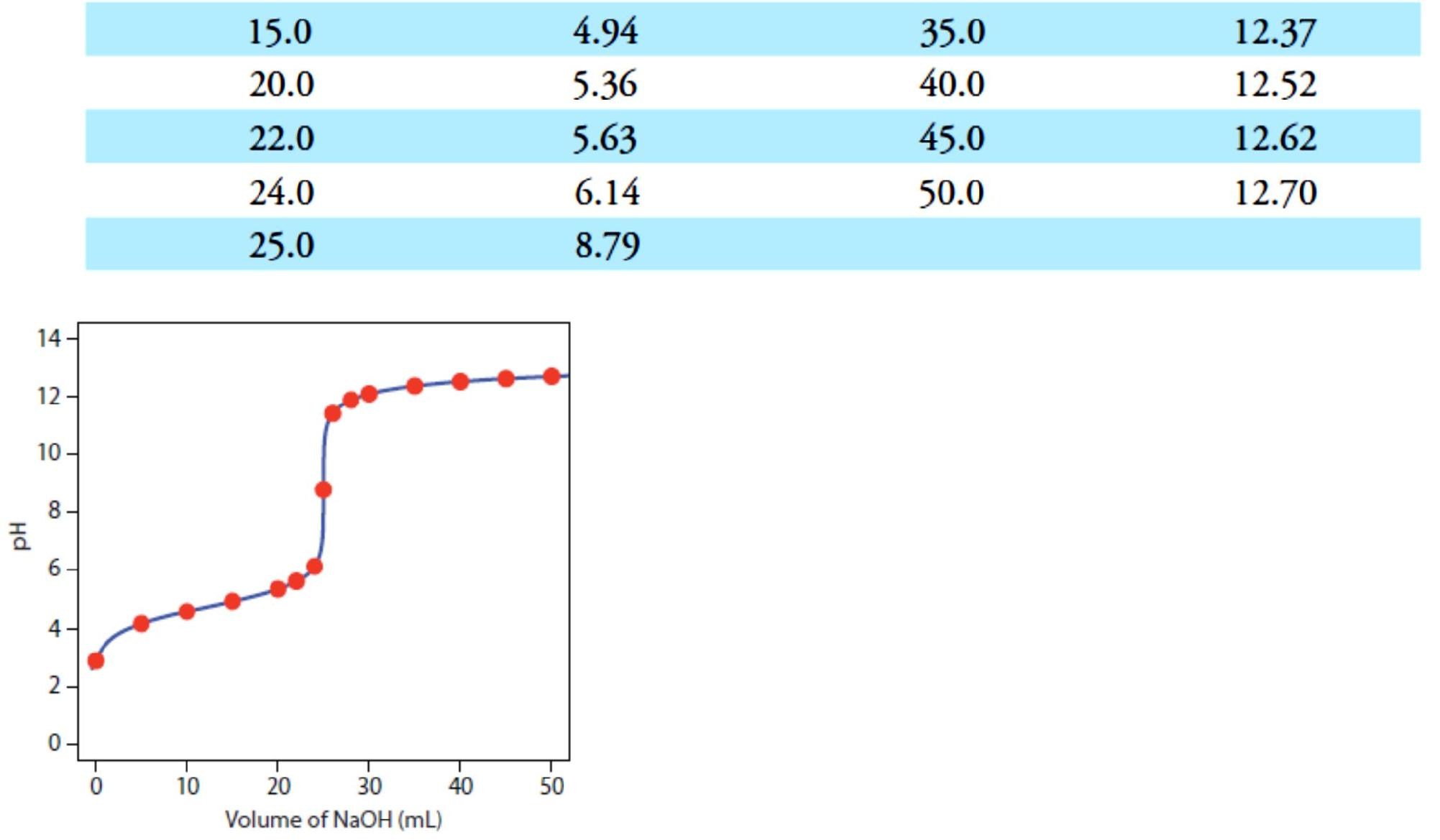
Figure 3 Titration curve for the titration of 50.0 mL of 0.100M CH3COOH with 0.200 M NaOH. The red points correspond

to the data in Table 2. The blue line shows the complete titration curve.

We can extend our approach for calculating a weak acid–strong base titration curve to reactions involving multiprotic acids or bases, and mixtures of acids or bases. As the complexity of the titration increases, however, the necessary calculations become more time consuming. Not surprisingly, a variety of algebraic1 and computer spreadsheet2 approaches have been described to aid in constructing titration curves.

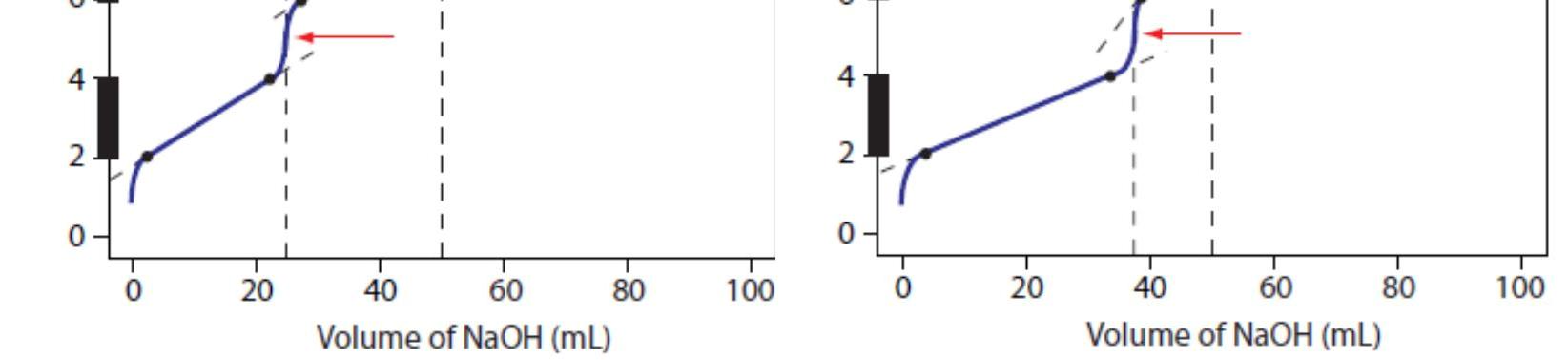
Figure 4a shows the titration curve for H2A, including the ladder diagram on the y-axis, the equivalence points at 25.0 mL and 50.0 mL, two points before each equivalence point, two points after the last equivalence point,and the straight-lines that help in sketching the final curve. Before the first equivalence point the pH is controlled by a buffer consisting of H2A and HA–. An HA–/A2– buffer controls the pH between the two equivalence points. After the second equivalence point the pH reflects the concentration of excess NaOH.

Figure 4b shows the titration curve for the mixture of HA and HB. Again, there are two equivalence points. In this case, however, the equivalence points are not equally spaced because the concentration of HA is greater than that for HB. Since HA is the stronger of the two weak acids it reacts first; thus, the pH before the first equivalence point is controlled by a buffer consisting of HA and A–. Between the two equivalence points the pH reflects the titration of HB and is determined by a buffer consisting of HB and B–. After the second equivalence point excess NaOH is responsible for the pH.

Date: 2015-01-29; view: 12206