Are Angular Quantities Vectors?

We can describe the position, velocity, and acceleration of a single particle by means of vectors. If the particle is confined to a straight line, however, we do not really need vector notation. Such a particle has only two directions available to it, and we can indicate these directions with plus and minus signs.

In the same way, a rigid body rotating about a fixed axis can rotate only clockwise or counterclockwise as seen along the axis, and again we can select between the two directions by means of plus and minus signs. The question arises: "Can we treat the angular displacement, velocity, and acceleration of a rotating body as vectors?" The answer is a qualified "yes"

In the same way, a rigid body rotating about a fixed axis can rotate only clock-

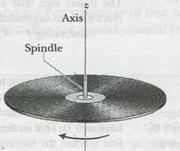Figure 1-l6a
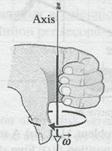Fig. 11-6c

wise or counterclockwise as seen along the axis, and again we can select between the two directions by means of plus and minus signs. The question arises: "Can we treat the angular displacement, velocity, and acceleration of a rotating body as vectors?" The answer is a qualified "yes"

Consider the angular velocity. Figure 1 l-6a shows a vinyl record rotating on a turntable. The record has a constant angular speed 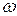= 33 rev/min) in the clock-wise direction. We can represent its angular velocity as a vector 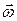pointing along the axis of rotation,. Here's how: We choose the length of this vector according to some convenient scale, for example, with 1 cm corresponding to 10 rev/min. Then we establish a direction for the vector 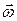by using a right-hand rule, as Fig. 11-6c shows: Curl your right hand about the rotating record, your fingers I pointing in the direction of rotation. Your extended thumb will then point in the direction of the angular velocity vector. If the record were to rotate in the opposite sense, the right-hand rule would tell you that the angular velocity vector then points in the opposite direction.

It is not easy to get used to representing angular quantities as vectors. We instinctively expect that something should be moving along the direction of a vector. That is not the case here. Instead, something (the rigid body) is rotating around the direction of the vector. In the world of pure rotation, a vector defines an axis of rotation, not a direction in which something moves. Nonetheless, the vector also defines the motion. The angular acceleration 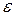is another vector, and it too obeys those rules.

Date: 2015-01-12; view: 1886