
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Relating the Linear and Angular Variables
In Section 4-7, we discussed uniform circular motion, in which a particle travels at constant linear speed  along a circle and around an axis of rotation. When a rigid body, such as a merry-go-round, rotates around an axis, each particle in the body moves in its own circle around that axis. Since the body is rigid, all the particles make one revolution in the same amount of time; that is, they all have the same angular speed
along a circle and around an axis of rotation. When a rigid body, such as a merry-go-round, rotates around an axis, each particle in the body moves in its own circle around that axis. Since the body is rigid, all the particles make one revolution in the same amount of time; that is, they all have the same angular speed 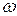 .
.
However, the farther a particle is from the axis, the greater the circumference of its circle is, and so the faster its linear speed  must be. You can notice this on a merry-go-round. You turn with the same angular speed
must be. You can notice this on a merry-go-round. You turn with the same angular speed 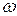 regardless of your distance from the center, but your linear speed
regardless of your distance from the center, but your linear speed  increases noticeably if you move to the outside edge of the merry-go-round.
increases noticeably if you move to the outside edge of the merry-go-round.
We often need to relate the linear variables 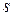 ,
,  , and
, and 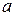 for a particular point in a rotating body to the angular variables
for a particular point in a rotating body to the angular variables 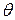 ,
, 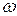 , and
, and 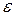 for that body. The two sets of variables are related by
for that body. The two sets of variables are related by 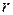 , the perpendicular distance of the point from the rotation axis. This perpendicular distance is the distance between the point and the rotation axis, measured along a perpendicular to the axis. It is also the radius
, the perpendicular distance of the point from the rotation axis. This perpendicular distance is the distance between the point and the rotation axis, measured along a perpendicular to the axis. It is also the radius 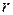 of the circle traveled by the point around the axis of rotation.
of the circle traveled by the point around the axis of rotation.
The Position
If a reference line on a rigid body rotates through an angle 0, a point within the body at a position 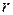 from the rotation axis moves a distance
from the rotation axis moves a distance 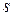 along a circular arc, where
along a circular arc, where 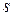 is given by Eq. 11-1:
is given by Eq. 11-1:
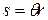 (radian measure). 11-17
(radian measure). 11-17

 This is the first of our linear-angular relations. Caution: The angle
This is the first of our linear-angular relations. Caution: The angle 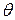 here must be measured in radians because Eq. 11-17 is itself the definition of angular measure in radians.
here must be measured in radians because Eq. 11-17 is itself the definition of angular measure in radians.

| |
|
The Speed
Differentiating Eq. 11-17 with respect to time - with 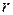 held constant - leads to
held constant - leads to
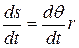
However, 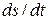 is the linear speed (the magnitude of the linear velocity) of the point in question, and
is the linear speed (the magnitude of the linear velocity) of the point in question, and 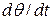 is the angular speed
is the angular speed 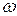 of the rotating body. So
of the rotating body. So
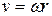 (radian measure). 11-18
(radian measure). 11-18
Caution: The angular speed 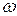 must be expressed in radian measure.
must be expressed in radian measure.
Equation 11-18 tells us that since all points within the rigid body have the same angular speed 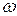 , points with greater radius
, points with greater radius 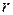 have greater linear speed
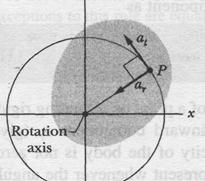
have greater linear speed  . Figure 1 l-9a reminds us that the linear velocity is always tangent to the circular path of the point in question.
. Figure 1 l-9a reminds us that the linear velocity is always tangent to the circular path of the point in question.
The Acceleration
Differentiating Eq. 11-18 with respect to time - again with 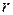 held constant-leads to
held constant-leads to

Here we run up against a complication. In Eq. 11-21,  represents only the part of the linear acceleration that is responsible for changes in the magnitude
represents only the part of the linear acceleration that is responsible for changes in the magnitude  of the linear velocity
of the linear velocity 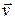 . Like
. Like 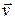 , that part of the linear acceleration is tangent to the path of the point in question. We call it the tangential component
, that part of the linear acceleration is tangent to the path of the point in question. We call it the tangential component 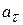 of the linear acceleration of the point, and we write
of the linear acceleration of the point, and we write
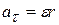 11-22 (radian measure),
11-22 (radian measure),
where 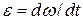 . Caution: The angular acceleration
. Caution: The angular acceleration 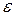 in Eq. 11-22 must be expressed in radian measure.
in Eq. 11-22 must be expressed in radian measure.
In addition, as Eq. 4-32 tells us, a particle (or point) moving in a circular path has a radial component of linear acceleration, 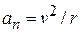 (directed radially inward), that is responsible for changes in the direction of the linear velocity
(directed radially inward), that is responsible for changes in the direction of the linear velocity 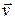 . By substituting for
. By substituting for  from Eq. 11-18, we can write this component as
from Eq. 11-18, we can write this component as
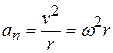 (radian measure).
(radian measure).
Thus, as Fig. 1 l-9b shows, the linear acceleration of a point on a rotating rigid body has, in general, two components. The radially inward component 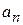 (given by Eq. 11-23) is present whenever the angular velocity of the body is not zero. The tangential component
(given by Eq. 11-23) is present whenever the angular velocity of the body is not zero. The tangential component 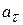 (given by Eq. 11-22) is present whenever the angular acceleration is not zero.
(given by Eq. 11-22) is present whenever the angular acceleration is not zero.
 11-6 Kinetic Energy of Rotation
11-6 Kinetic Energy of Rotation
The rapidly rotating blade of a table saw certainly has kinetic energy due to that rotation. How can we express the energy? We cannot apply the familiar formula  to the saw as a whole because that would only give us the kinetic energy of the saw's center of mass, which is zero.
to the saw as a whole because that would only give us the kinetic energy of the saw's center of mass, which is zero.
Instead, we shall treat the table saw (and any other rotating rigid body) as a collection of particles with different speeds. We can then add up the kinetic energies of all the particles to find the kinetic energy of the body as a whole. In this way we obtain, for the kinetic energy of a rotating body,
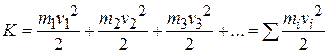
in which 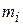 is the mass of the
is the mass of the 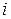 -th particle and
-th particle and 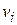 is its speed. The sum is taken over all the particles in the body.
is its speed. The sum is taken over all the particles in the body.
The problem with Eq. 11-24 is that 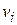 is not the same for all particles. We solve this problem by substituting for
is not the same for all particles. We solve this problem by substituting for  from Eq. 11-18 (
from Eq. 11-18 ( 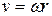 ), so that we have
), so that we have
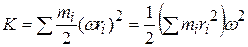
in which 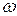 is the same for all particles.
is the same for all particles.
The quantity in parentheses on the right side of Eq. 11-25 tells us how the mass of the rotating body is distributed about its axis of rotation. We call that quantity the rotational inertia (or moment of inertia) 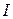 of the body with respect to the axis of rotation. It is a constant for a particular rigid body and a particular rotation axis. (That axis must always be specified if the value of
of the body with respect to the axis of rotation. It is a constant for a particular rigid body and a particular rotation axis. (That axis must always be specified if the value of 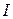 is to be meaningful.)
is to be meaningful.)
We may now write
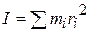 11-26
11-26
and substitute into Eq. 11-25
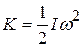 11-27
11-27
as the expression we seek. Because we have used the relation 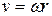 in deriving Eq. 11-27,
in deriving Eq. 11-27, 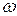 must be expressed in radian measure. The SI unit for
must be expressed in radian measure. The SI unit for 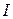 is the kilogram-square meter (kg • m2).
is the kilogram-square meter (kg • m2).
Equation 11-27, which gives the kinetic energy of a rigid body in pure rotation, is the angular equivalent of the formula  , which gives the kinetic energy of a rigid body in pure translation. In both formulas there is a factor of 1/2. Where mass M appears in one equation,
, which gives the kinetic energy of a rigid body in pure translation. In both formulas there is a factor of 1/2. Where mass M appears in one equation, 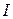 (which involves both mass and its distribution) appears in the other. Finally, each equation contains as a factor the square of a speed - translational or rotational as appropriate. The kinetic energies of translation and of rotation are not different kinds of energy. They are both kinetic energy, expressed in ways that are appropriate to the motion at hand.
(which involves both mass and its distribution) appears in the other. Finally, each equation contains as a factor the square of a speed - translational or rotational as appropriate. The kinetic energies of translation and of rotation are not different kinds of energy. They are both kinetic energy, expressed in ways that are appropriate to the motion at hand.
We noted previously that the rotational inertia of a rotating body involves not only its mass but also how that mass is distributed. Here is an example that you can literally feel. Rotate a long, fairly heavy rod (a pole, a length of lumber, or something similar), first around its central (longitudinal) axis (Fig. 11-1 la) and then around an axis perpendicular to the rod and through the center (Fig. 11-116). Both rotations involve the very same mass, but the first rotation is much easier than the second. The reason is that the mass is distributed much closer to the rotation axis in the first rotation. As a result, the rotational inertia of the rod is much smaller in Fig. 11-Ø than in Fig. 11-1 lb. In general, smaller rotational inertia means easier rotation.
Parallel-Axis Theorem
Suppose we want to find the rotational inertia / of a body of mass  about a given axis. In principle, we can always find / with the integration of Eq. 11-28. However, there is a shortcut if we happen to already know the rotational inertia
about a given axis. In principle, we can always find / with the integration of Eq. 11-28. However, there is a shortcut if we happen to already know the rotational inertia  of the body about a parallel axis that extends through the body's center of mass. Let
of the body about a parallel axis that extends through the body's center of mass. Let 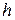 be the perpendicular distance between the given axis and the axis through the center of mass (remember these two axes must be parallel). Then the rotational inertia
be the perpendicular distance between the given axis and the axis through the center of mass (remember these two axes must be parallel). Then the rotational inertia 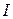 about the given axis is
about the given axis is
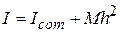 (parallel-axis theorem). (11-29)
(parallel-axis theorem). (11-29)
This equation is known as the parallel-axis theorem. We shall now prove it.
Proof of the Parallel-Axis Theorem
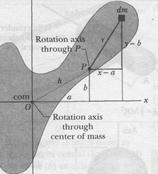 Fig. 11-12
Fig. 11-12
|
Let Î be the center of mass of the arbitrarily shaped body shown in cross section in Fig. 11-12. Place the origin of the coordinates at O. Consider an axis through O perpendicular to the plane of the figure, and another axis through point P parallel to the first axis. Let the x and ó coordinates of P be a and b.
Let 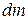 be a mass element with the general coordinates x and y. The rotational inertia of the body about the axis through P is then, from Eq. 11-28,
be a mass element with the general coordinates x and y. The rotational inertia of the body about the axis through P is then, from Eq. 11-28,

which we can rearrange as
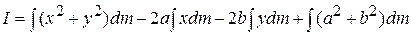 11-30
11-30
From the definition of the center of mass (Eq. 9-9), the middle two integrals of Eq. 11-30 give the coordinates of the center of mass (multiplied by a constant) and thus must each be zero. Because 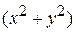 is equal to
is equal to  , where
, where  is the distance from Î to
is the distance from Î to 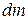 , the first integral is simply
, the first integral is simply  , the rotational inertia of the body about an axis through its center of mass. Inspection of Fig. 11-12 shows that the last term in Eq. 11-30 is
, the rotational inertia of the body about an axis through its center of mass. Inspection of Fig. 11-12 shows that the last term in Eq. 11-30 is  , where
, where  is the body's total mass. Thus, Eq. 11-30 reduces to Eq. 11-29, which is the relation that we set out to prove.
is the body's total mass. Thus, Eq. 11-30 reduces to Eq. 11-29, which is the relation that we set out to prove.
Date: 2015-01-12; view: 4135
| <== previous page | | | next page ==> |
| Are Angular Quantities Vectors? | | | ÒÎ FIND MOMENT OF INERTIA OF A RIGID BODY |