
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
ROTATIONAL MOTION
11-1 Translation and Rotation
The graceful movement of figure skaters can be used to illustrate two kinds of pure, or unmixed, motion. If a skater is gliding across the ice in a straight line with constant speed, her motion is one of pure translation. If she spinning at a constant rate about a vertical axis, in a motion of pure rotation. Translation is motion along a straight line, which has been our focus up to now. Rotation is the motion of wheels, gears, motors, planets, the hands of clocks, the rotors of jet engines, and the blades of helicopters. It is our focus in this chapter.
11-2 The Rotational Variables
We wish to examine the rotation of a rigid body about a fixed axis. A rigid body is a body that can rotate with all its parts locked together and without any change in its shape. A fixed axis means that the rotation occurs about an axis that does not move. Thus, we shall not examine an object like the Sun, because the parts of the Sun (a ball of gas) are not locked together. We also shall not examine an object like a bowling ball rolling along a bowling alley, because the ball rotates about an axis that moves (the ball's motion is a mixture of rotation and translation).
Figure 11-2 shows a rigid body of arbitrary shape in rotation about a fixed axis, called the axis of rotation or the rotation axis. Every point of the body moves in a circle whose center lies on the axis of rotation, and every point moves through the same angle during a particular time interval. In pure translation, every point of the body moves in a straight line, and every point moves through the same linear distance during a particular time interval. (Comparisons between angular and linear motion will appear throughout this chapter.)
We deal now - one at a time - with the angular equivalents of the linear quantities position, displacement, velocity, and acceleration.
Angular Position
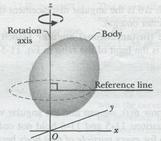 Figure 11-2
Figure 11-2
|
Figure 11-2 shows a reference line, fixed in the body, perpendicular to the rotation axis, and rotating with the body. The angular position of this line is the angle of the line relative to a fixed direction, which we take as the zero angular position. In Fig. 11-3, the angular position 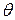 is measured relative to the positive direction of the
is measured relative to the positive direction of the  axis. From geometry, we know that
axis. From geometry, we know that 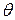 is
is
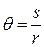
Here 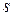 is the length of arc (or the arc distance) along a circle and between the
is the length of arc (or the arc distance) along a circle and between the  axis (the zero angular position) and the reference line;
axis (the zero angular position) and the reference line; 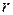 is the radius of that circle.
is the radius of that circle.
An angle defined in this way is measured in radians (rad) rather than in revolutions (rev) or degrees. The radian, being the ratio of two lengths, is a pure number and thus has no dimension. Because the circumference of a circle of radius 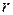 is
is 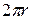 , there are
, there are 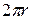 radians in a complete circle:
radians in a complete circle:
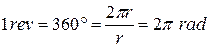
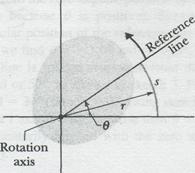 Fig. 11-3
Fig. 11-3
|
and thus 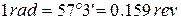
We do not reset 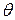 to zero with each complete rotation of the reference line about the rotation axis. If the reference line completes two revolutions from the zero angular position, then the angular position
to zero with each complete rotation of the reference line about the rotation axis. If the reference line completes two revolutions from the zero angular position, then the angular position 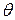 of the line is
of the line is
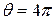 rad.
rad.
 For pure translational motion along the
For pure translational motion along the  direction, we can know all there is to know about a moving body if we are given
direction, we can know all there is to know about a moving body if we are given 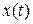 , its position as a function of time. Similarly, for pure rotation, we can know all there is to know about a rotating body if we are given
, its position as a function of time. Similarly, for pure rotation, we can know all there is to know about a rotating body if we are given  , the angular position of the body's reference line as a function of time.
, the angular position of the body's reference line as a function of time.
Angular Displacement
If the body of Fig. 11-3 rotates about the rotation axis as in Fig. 11-4, changing the angular position of the reference line from 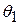 to
to 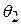 , the body undergoes an angular displacement
, the body undergoes an angular displacement 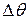 given by
given by
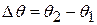
This definition of angular displacement holds not only for the rigid body as a whole but also for every particle within that body because the particles are all locked together.
If a body is in translational motion along an  axis, its displacement
axis, its displacement 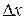 is either positive or negative, depending on whether the body is moving in the positive or negative direction of the axis. Similarly, the angular displacement
is either positive or negative, depending on whether the body is moving in the positive or negative direction of the axis. Similarly, the angular displacement 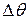 of a rotating body is either positive or negative, according to the following rule:
of a rotating body is either positive or negative, according to the following rule:
An angular displacement in the counterclockwise direction is positive, and one in the clockwise direction is negative.
Angular Velocity
Suppose (see Fig. 11-4) that our rotating body is at angular position 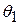 at time
at time 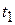 and at angular position
and at angular position 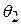 at time
at time 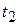 . We define the average angular velocity of the body in the time interval
. We define the average angular velocity of the body in the time interval 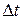 from
from 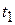 to
to 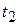 to be
to be
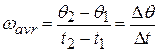 11 -5
11 -5
in which 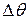 is the angular displacement that occurs during
is the angular displacement that occurs during 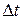 (
( 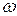 is the lowercase Greek letter omega).
is the lowercase Greek letter omega).
The (instantaneous) angular velocity 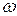 , with which we shall be most concemed, is the limit of the ratio in Eq. 11 -5 as
, with which we shall be most concemed, is the limit of the ratio in Eq. 11 -5 as 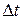 approaches zero. Thus,
approaches zero. Thus,
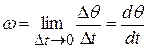 11 -6
11 -6


 If we know
If we know  , we can find the angular velocity
, we can find the angular velocity 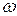 by differentiation.
by differentiation.
 Fig. 11-4
Fig. 11-4
|
Equations 11-5 and 11-6 hold not only for the rotating rigid body as a whole but also for every particle of that body because the particles are all locked together. The unit of angular velocity is commonly the radian per second (rad/s) or the revolution per second (rev/s).
If a particle moves in translation along an  axis, its linear velocity
axis, its linear velocity  is either positive or negative, depending on whether the particle is moving in the positive or negative direction of the axis. Similarly, the angular velocity
is either positive or negative, depending on whether the particle is moving in the positive or negative direction of the axis. Similarly, the angular velocity 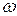 of a rotating rigid body is either positive or negative, depending on whether the body is rotating counterclockwise (positive) or clockwise (negative). The magnitude of an angular velocity is called the angular speed, which is also represented with
of a rotating rigid body is either positive or negative, depending on whether the body is rotating counterclockwise (positive) or clockwise (negative). The magnitude of an angular velocity is called the angular speed, which is also represented with 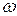 .
.
Angular Acceleration
If the angular velocity of a rotating body is not constant, then the body has an angular acceleration. Let 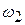 and
and 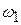 be its angular velocities at times
be its angular velocities at times 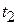 and
and 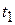 , respectively, The average angular acceleration of the rotating body in the interval from
, respectively, The average angular acceleration of the rotating body in the interval from 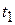 to
to 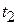 is defined as
is defined as
 11 -7
11 -7
in which  is the change in the angular velocity that occurs during the time interval
is the change in the angular velocity that occurs during the time interval 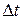 . The (instantaneous) angular acceleration
. The (instantaneous) angular acceleration 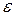 , with which we shall be most concerned, is the limit of this quantity as
, with which we shall be most concerned, is the limit of this quantity as 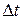 approaches zero. Thus,
approaches zero. Thus,
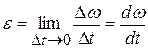 11-8
11-8
Equations 11-7 and 11-8 hold not only for the rotating rigid body as a whole but also for every particle of that body. The unit of angular acceleration is commonly the radian per second-squared (rad/s2) or the revolution per second-squared (rev/s2).
Date: 2015-01-12; view: 1581
| <== previous page | | | next page ==> |
| Type C. On Work-energy theorem | | | Are Angular Quantities Vectors? |