Work Done by a General Variable force

One-Dimensional Analysis

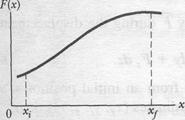
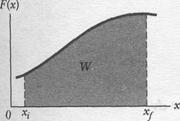
Let us return to the situation of Fig. 7-2 but now consider the force to be directed along the axis and the force magnitude to vary with position . Thus, as the bead (particle) moves, the magnitude of the force doing work on it changes. Only the magnitude of this variable force changes, not its direction, and the magnitude at any position does not change with time.

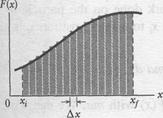
Figure l-\2a shows a plot of such a one-dimensional variable force. We want an expression for the work done on the particle by this force as the particle moves from an initial point 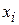, to a final point 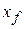. However, we cannot use Eq. 7-7 because it applies only for a constant force . Here, again, we shall use calculus. We divide the area under the curve of Fig. 7-12a into a number of narrow strips of

width 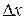(Fig. 1-I2b). We choose 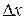small enough to permit us to take the force as being reasonably constant over that interval. We let 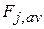be the average value of within the 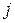-th interval. Then in Fig. 7-12b, 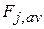is the height of the 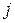-th strip.

With 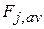considered constant, the increment (small amount) of work ,-done by the force in the 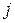-th interval is now approximately given by Eq. 7-7 and is

(7-29)

In Fig. 7-12b, , is then equal to the area of the 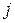-th rectangular, shaded strip.

To approximate the total work 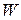done by the force as the particle moves from 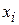to 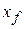, we add the areas of all the strips between 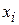and 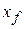in Fig. 7-12b:

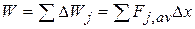(7-30)

Equation 7-30 is an approximation because the broken "skyline" formed by the tops of the rectangular strips in Fig. 1-I2b only approximates the actual curve of .

We can make the approximation better by reducing the strip width Ал and using more strips, as in Fig. 7-12c. In the limit, we let the strip width approach zero; the number of strips then becomes infinitely large and we have, as an exact result,

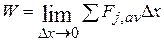(7-31)

This limit is exactly what we mean by the integral of the function F(x) between the limits 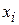, and 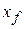. Thus, Eq. 7-31 becomes

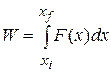(7-32)

If we know the function , we can substitute it into Eq. 7-32, introduce the proper limits of integration, carry out the integration, and thus find the work.

Three-Dimensional Analysis

Consider now a particle that is acted on by a three-dimensional force

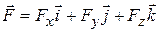(7-33

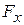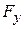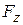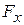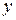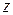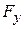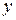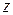in which the components , , and can depend on the position of the particle that is, they can be functions of that position. However, we make three simplifications: may depend on but not on or , may depend on but not on or , and 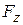may depend on 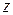but not on or 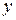. Now let the particle move through an incremental displacement

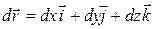(7-34)

The increment of work done on the particle by during the displacement 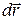is, by Eq. 7-8,

(7-35)

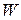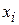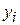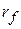The work done by while the particle moves from an initial position with coordinates ( , , ) to a final position with coordinates ( 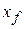, , 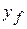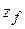) is then

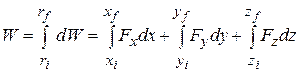(7-36)

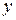If has only an component, then the and 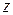terms in Eq. 7-36 are zero and the equation reduces to Eq. 7-32.

Date: 2015-01-12; view: 1338