Work-Kinetic Energy Theorem with a Variable Force

Equation 7-32 gives the work done by a variable force on a particle in a one-dimensional situation. Let us now make certain that the work calculated with Eq. 7-32 is indeed equal to the change in kinetic energy of the particle, as the work-kinetic energy theorem states.

Consider a particle of mass 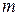, moving along the axis and acted on by a net force that is directed along that axis. The work done on the particle by this force as the particle moves from an initial position 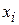to a final position 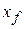is given by Eq. 7-32 as

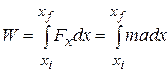(7-37)

in which we use Newton's second law to replace with 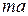. We can write the quantity

(7-38)

in Eq. 7-37 as

From the "chain rule" of calculus, we have

(7-39)

and Eq. 7-38 becomes

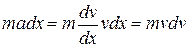(7-40)

Substituting (7-40) into 7-37 yields

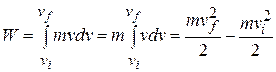(7-41)

Note that when we change the variable from to we are required to express the limits on the integral in terms of the new variable. Note also that because the mass m is a constant, we are able to move it outside the integral.

Recognizing the terms on the right side of Eq. 7-41 as kinetic energies allows us to write this equation as

which is the work-kinetic energy theorem.

Sample Problem 7-9

Force 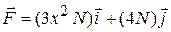, with in meters, acts on a particle, changing only the kinetic energy of the particle. How much work is done on the particle as it moves from coordinates (2 m, 3 m) to (3 m, 0 m)? Does the speed of the particle increase, decrease, or remain the same?

SOLUTION; The Key Idea here is that the force is a variable force because its component depends on the value of . Thus, we cannot use Eqs. 7-7 and 7-8 to find the work done. Instead, we must use Eq. 7-36 to integrate the force:

The positive result means that energy is transferred to the particle by force F. Thus, the kinetic energy of the particle increases, and so must its speed.

7-7 Power

A contractor wishes to lift a load of bricks from the sidewalk to the top of a building by means of a winch. We can now calculate how much work the force applied by the winch must do on the load to make the lift. The contractor, however, is much more interested in the rate at which that work is done. Will the job take 5 minutes (acceptable) or a week (unacceptable)?

The time rate at which work is done by a force is said to be the power due to the force. If an amount of work 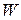is done in an amount of time 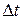by a force, the average power due to the force during that time interval is

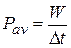(7-42)

The instantaneous power is the instantaneous time rate of doing work, which we can write as

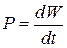(7-42)

Suppose we know the work done by a force as a function of time. Then to get the instantaneous power at, say, time 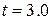s during the work, we would first take the time derivative of , and then evaluate the result for 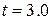s.

The SI unit of power is the joule per second. This unit is used so often that it has a special name, the watt (W), after James Watt, who greatly improved the rate at which steam engines could do work. In the British system, the unit of power is the foot-pound per second. Often the horsepower is used. Some relations among these units are

And

W.

We can also express the rate at which a force does work on a particle (or particle like object) in terms of that force and the particle's velocity. For a particle that i! moving along a straight line (say, the x axis) and is acted on by a constant force / directed at some angle 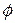to that line, Eq. 7-43 becomes

,

or

Reorganizing the right side of Eq. 7-47 as the dot product 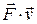, we may also write Eq. 7-47 as

For example, the truck in Fig. 7-13 exerts a force 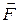on the trailing load, which has velocity 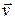at some instant. The instantaneous power due to 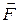is the rate at which 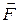does work on the load at that instant and is given by Eqs. 7-47 and 7-48. Saying that this power is "the power of the truck" is often acceptable, but we should keep in mind what is meant: Power is the fate at which the applied force does work.

•CHECKPOINT 5: A block moVes with uniform circular motion because a cord tied to the block is anchored at the center of a circle. Is the power due to the force on the block from the cord positive, negative, or zero?

Sample Problem 7-10

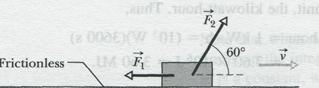
Figure 7-14 shows constant forces and acting on a box as the box slides rightward across a frictionless floor. Force is horizontal, with magnitude 2.0 N; force is angled upward by 60° to the floor and has magnitude 4.0 N. The speed v of the box at a certain instant is 3.0 m/s.

(a) What is the power due to each force acting on the box at that instant, and what is the net power? Is the net power changing at that instant?

SOLUTION: A Key Idea here is that we want an instantaneous power, not an average power over a time period. Also, we know the particle's velocity (rather than the work done on it). Therefore, we use Eq. 7-47 for each force. For force at angle 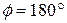° to velocity

Fig. 7-14 Sample Problem 7-10. Two forces F_x and F₂ act on a box that slides rightward across a frictionless floor. The velocity of the box is v*.

Date: 2015-01-12; view: 1841