Work Done by a Gravitational force

We next examine the work done on an object by a particular type of force - namely, the gravitational force acting on it. Figure 7-6 shows a particle-like tomato of mass 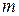that is thrown upward with initial speed 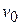and thus with initial kinetic energy 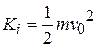. As the tomato rises, it is slowed by a gravitational force ; that is, the tomato's kinetic energy decreases because does work on the tomato as it rises.

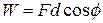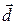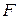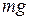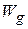Because we can treat the tomato as a particle, we can use Eq. 7-7 ( ) to express the work done during a displacement . For the force magnitude , we use as the magnitude of . Thus, the work done by the gravitational force , is

work done by gravitational force (7-12)

For a rising object, force is directed opposite the displacement 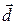, as indicated in Fig. 7-6. Thus, 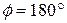and

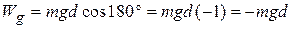(7-13)

The minus sign tells us that during the object's rise, the gravitational force on the object transfers energy in the amount 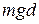from the kinetic energy of the object. This is consistent with the slowing of the object as it rises.

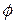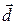After the object has reached its maximum height and is falling back down, the angle between force and displacement is zero. Thus,

The plus sign tells us that the gravitational force now transfers energy in the amount 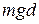to the kinetic energy of the object. This is consistent with the speeding up of the object as it falls. (Actually, as we shall see in Chapter 8, energy transfers associated with lifting and lowering an object involve not just the object, but the full object-Earth system. Without Earth, of course, "lifting" would be meaningless.)

EXAMPLE 7—3 A child of weight 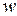sits on a swing of length , as shown in Fig. 7-7. A variable horizontal force , which starts at zero and gradually increases, is used to pull the child very slowly (so that equilibrium exists at all times) until the ropes make an angle 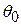with the vertical. Calculate the work of the force .

SOLUTION The body is in equilibrium, so the sum of the horizontal forces equals zero:

.

The sum of the vertical forces is also zero:

.

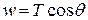Dividing these two equations, we find

.

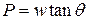The point of application of swings through the arcs. Since 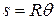, 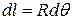and

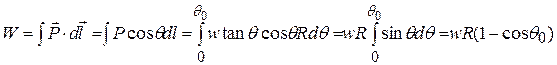
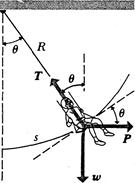
If 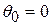, there is no displacement; in that case 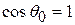and 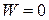, as expected. If 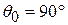°, then 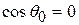and 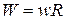. In that case the work is the same as though the body had been lifted straight up a distance by a force equal to its weight 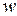. In fact, as you should verify, the quantity is the increase in the height of the body during the displacement; so for any value of 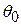, the work done by force is the change in height multiplied by the weight. We will prove this result more generally in Section 7—5.

EXAMPLE 7—10 In Jules Verne's story "From the Earth to the Moon" (written in 1865) three men were shot to the moon in a shell fired from a giant cannon sunk in the earth in Florida. What muzzle velocity would be needed (a) to raise a total mass m to a height above the earth equal to the earth's radius; (b) to escape from the earth completely? To simplify the calculation, neglect the gravitational pull of the moon.

SOLUTION

a) In Eq. (7-23), let 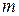be the total projectile mass and let 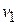be the initial velocity.

Then 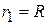, , 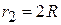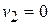and

or

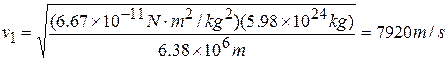
Then

b) When is the escape velocity, , , 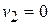. Then

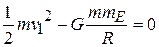or ,

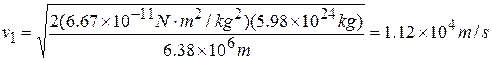
Note that the speed of an earth satellite in a circular orbit of radius just slightly greater than is, from Eq. (6—22), the same as the result of part (a), and that the escape velocity is larger than this by exactly a factor of .

Work Done in Lifting and Lowering an Object

Now suppose we lift a particle-like object by applying a vertical force to it. During the upward displacement, our applied force does positive work 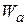on the object while the gravitational force does negative work 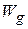on it. Our force tends to transfer energy to the object while the gravitational force tends to transfer energy from it. By Eq. 7-10, the change 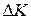in the kinetic energy of the object due to these two energy transfers is

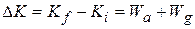(7-15)

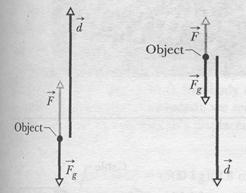
in which 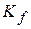is the kinetic energy at the end of the displacement and 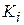is that at the start of the displacement. This equation also applies if we lower the object, but then the gravitational force tends to transfer energy to the object while our force tends to transfer energy from it.

In one common situation the object is stationary before and after the lift - for example, when you lift a book from the floor to a shelf. Then 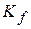and 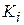are both zero, and Eq. 7-15 reduces to

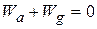
Or

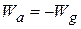(7-16)

Note that we get the same result if 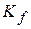and 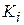are not zero but are still equal. Either way, the result means that the work done by the applied force is the negative of the work done by the gravitational force; that is, the applied force transfers the same amount of energy to the object as the gravitational force transfers from the object. Using Eq. 7-12, we can rewrite Eq. 7-16 as

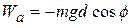(work in lifting and lowering; 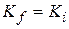(7-17)

with 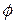being the angle between and 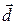. If the displacement is vertically upward (Fig. 7-7 a), then 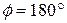and the work done by our force equals 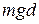. If the displacement is vertically downward (Fig. 1-lb), then and the work done by the applied force equals .

Equations 7-16 and 7-17 apply to any situation in which an object is lifted or lowered, with the object stationary before and after the lift. They are independent of the magnitude of the force used. For example, when Chemerkin made his record-breaking lift, his force on the object he lifted varied considerably during the lift. Still, because the object was stationary before and after the lift, the work he did is given by Eqs. 7-16 and 7-17, where, in Eq. 7-17, mg is the weight of the object he lifted and d is the distance he lifted it.

7-5 Work Done by a Spring force

We next want to examine the work done on a particle-like object by a particular type of variable force - namely, a spring force, the force from a spring. Many forces in nature have the same mathematical form as the spring force. Thus, by examining this one force, you can gain an understanding of many others.

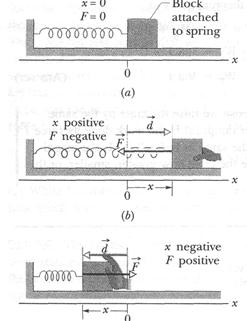
The Spring Force

Figure 7-lOa shows a spring in its relaxed state - that is, neither compressed nor extended. One end is fixed, and a particle-like object, say, a block, is attached to the other, free end. If we stretch the spring by pulling the block to the right as in Fig. 7- 10b, the spring pulls on the block toward the left. (Because a spring's force acts to restore the relaxed state, it is sometimes said to be a restoring force.) If we compress the spring by pushing the block to the left as in Fig. 7-10c, the spring now pushes on the block toward the right.

To a good approximation for many springs, the force from a spring is proportional to the displacement 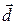of the free end from its position when the spring is in the relaxed state. The spring force is given by

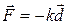(Hooke's law), (7-20)

which is known as Hooke's law after Robert Hooke, an English scientist of the late 1600s. The minus sign in Eq. 7-20 indicates that the spring force is always opposite in direction from the displacement of the free end. The constant 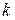is called the spring constant (or force constant) and is a measure of the stiffness of the spring. The larger 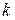is, the stiffer the spring; that is, the stronger will be its pull or push for a given displacement. The SI unit for 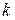is the newton per meter.

In Fig. 7-10 an axis has been placed parallel to the length of a spring, with the origin ( 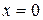) at the position of the free end when the spring is in its relaxed state. For this common arrangement, we can write Eq. 7-20 as

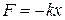(Hooke's law), (7-21)

If is positive (the spring is stretched toward the right on the axis), then 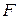is negative (it is a pull toward the left). If is negative (the spring is compressed toward the left), then 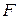is positive (it is a push toward the right).

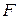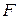Note that a spring force is a variable force because its magnitude and direction depend on the position of the free end; can be symbolized as . Also note that Hooke's law is a linear relationship between and .

The Work Done by a Spring Force

To find an expression for the work done by the spring force as the block in Fig. 7-10a moves, let us make two simplifying assumptions about the spring. (1) It is massless; that is, its mass is negligible compared to the block's mass. (2) It is an ideal spring; that is, it obeys Hooke's law exactly. Let us also assume that the contact between the block and the floor is frictionless and that the block is particle-like.

We give the block a rightward jerk to get it moving, and then leave it alone. As the block moves rightward, the spring force 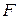does work on the block, decreasing the kinetic energy and slowing the block. However, we cannot find this work by using Eq. 7-7 ( 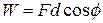) because that equation assumes a constant force. The spring force is a variable force.

To find the work done by the spring, we use calculus. Let the block's initial position be 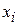and its later position 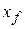. Then divide the distance between those two positions into many segments, each of tiny length 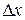. Label these segments, starting from 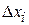as segments 1, 2, and so on. As the block moves through a segment, the spring force hardly varies because the segment is so short that hardly varies. Thus, we can approximate the force magnitude as being constant within the segment. Label these magnitudes as 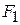in segment 1, 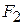in segment 2, and so on.

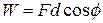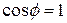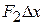With the force now constant in each segment, we can find the work done within each segment by using Eq. 7-7 ( ). Here , so . Then the work done is in segment 1, in segment 2, and so on. The net work done by the spring, from 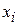- to 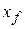, is the sum of all these works:

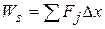, (7-22)

where 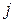labels the segments. In the limit as 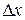goes to zero, Eq. 7-22 becomes

(7-23)

Substituting for 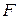from Eq. 7-21, we find

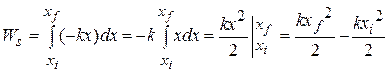
This work done by the spring force can have a positive or negative value, depending on whether the net transfer of energy is to or from the block as the block moves from 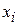to 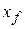,. Caution: The final position 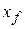appears in the second term on the right side of Eq. 7-25. Therefore, Eq. 7-25 tells us:

Work is positive if the block ends up closer to the relaxed position ( 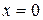) than it was initially. It is negative if the block ends up farther away from 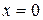. It is zero if the block ends up at the same distance from .

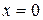If 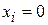and if we call the final position , then Eq. 7-25 becomes

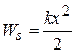(work by a spring force). (7-26)

The Work Done by an Applied force

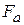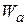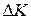Now suppose that we displace the block along the axis while continuing to apply a force to it. During the displacement, our applied force does work on the block while the spring force does work . By Eq. 7-10, the change in the kinetic energy of the block due to these two energy transfers is

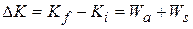(7-27)

in which K_f is the kinetic energy at the end of the displacement and K_t is that at the start of the displacement. If the block is stationary before and after the displacement, then K_f and K_t are both zero and Eq. 7-27 reduces to

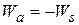(7-28)

If a block that is attached to a spring is stationary before and after a displacement, then the work done on it by the applied force displacing it is the negative of the work done on it by the spring force.

Date: 2015-01-12; view: 1428