
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Motion in Two or Three Dimensions
This chapter extends the material of the preceding two chapters to two and three dimensions. Many of the ideas of previous chapter, such as position, velocity, and acceleration, are used here, but they are now a little more complex because of the extra dimensions.
1.2 Position and Displacement
One general way of locating a particle (or particle-like object) is with a position vector 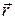 , which is a vector that extends from a reference point (usually the origin of a coordinate system) to the particle. In the unit-vector notation,
, which is a vector that extends from a reference point (usually the origin of a coordinate system) to the particle. In the unit-vector notation, 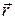 can be written
can be written
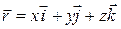 , (4-1)
, (4-1)
where 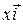 ,
, 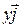 , and
, and 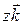 are the vector components of
are the vector components of 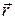 , and the coefficients
, and the coefficients  ,
, 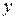 , and
, and 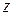 are its scalar components.
are its scalar components.
The coefficients  ,
, 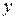 , and
, and 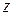 give the particle's location along the coordinate axes and relative to the origin; that is, the particle has the rectangular coordinates (
give the particle's location along the coordinate axes and relative to the origin; that is, the particle has the rectangular coordinates (  ,
, 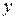 ,
,  ). For instance, Fig. 4-1 shows a particle with position vector
). For instance, Fig. 4-1 shows a particle with position vector
 (4-2)
(4-2)
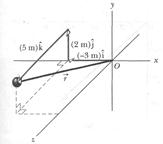 Fig. 4-1
Fig. 4-1
|
and rectangular coordinates 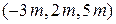 . Along the
. Along the  axis the particle is 3 m from the origin, in the
axis the particle is 3 m from the origin, in the  direction. Along the
direction. Along the 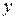 axis it is 2 m from the origin, in the
axis it is 2 m from the origin, in the 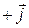 direction. Along the
direction. Along the 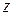 axis it is 5 m from the origin, in the
axis it is 5 m from the origin, in the 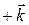 direction.
direction.
As a particle moves, its position vector changes in such a way that the vector always extends to the particle from the reference point (the origin). If the position vector changes, say, from 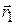 to
to 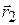 during a certain time interval, then the particle's displacement
during a certain time interval, then the particle's displacement 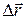 during that time interval is
during that time interval is
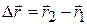 (4-2)
(4-2)
Using the unit-vector notation, we can rewrite this displacement as
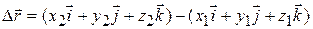
or as
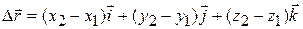 (4-3)
(4-3)
where coordinates (  ,
, 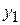 ,
, 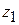 ) correspond to position vector
) correspond to position vector 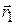 and coordinates (
and coordinates (  ,
, 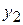 ,
, 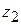 ) correspond to position vector
) correspond to position vector 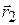 . We can also rewrite the displacement by substituting
. We can also rewrite the displacement by substituting 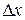 for
for 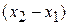 ,
, 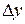 for
for 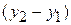 , and
, and 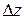 for
for 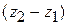 :
:
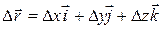 (4-3)
(4-3)
Example 4-1
In Fig. 4-2, the position vector for a particle is initially

 Fig. 4-2
Fig. 4-2
|
and then later is
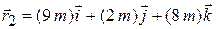 .
.
What is the particle's displacement 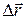 from
from 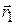 to
to 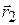 ?
?
Solution. The Key Idea is that the displacement 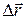 is obtained by subtracting the initial position vector
is obtained by subtracting the initial position vector 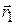 from the later position vector
from the later position vector 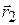 . That is most easily done by components:
. That is most easily done by components:
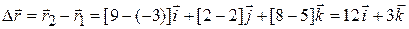 (Answer)
(Answer)
This displacement vector is parallel to the  plane, because it lacks any
plane, because it lacks any  component, a fact that is easier to see in the numerical result than in Fig. 4-2.
component, a fact that is easier to see in the numerical result than in Fig. 4-2.
Sample Problem 4-2
A rabbit runs across a parking lot on which a set of coordinate axes has been drawn. The coordinates of the rabbit's position as functions of time  are given by
are given by
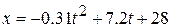 (4-5)
(4-5)
And  , (4-6)
, (4-6)
with  in seconds and
in seconds and  and
and 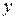 in meters.
in meters.
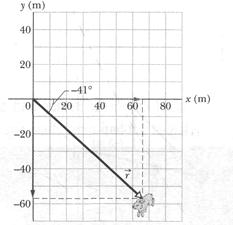
(a) At 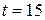 s, what is the rabbit's position vector
s, what is the rabbit's position vector 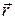 in unit-vector notation and as a magnitude and an angle?
in unit-vector notation and as a magnitude and an angle?
Solution. The Key Idea here is that the  and
and  coordinates of the rabbit's position, as given, are the scalar components of the rabbit's position vector
coordinates of the rabbit's position, as given, are the scalar components of the rabbit's position vector  . Thus, we can write
. Thus, we can write
|
(We write 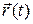 rather than
rather than 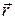 because the components are functions of
because the components are functions of  , and thus
, and thus 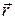 is also.)
is also.)
At 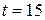 s, the scalar components are
s, the scalar components are
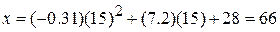 m,
m,
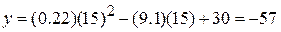 m.
m.
Thus, at
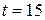 s,
s, 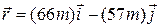 (Answer)
(Answer)
To get the magnitude and angle of 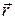 , we can use a vector-capable calculator, or we can write
, we can use a vector-capable calculator, or we can write
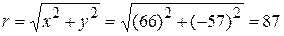 m. (Answer)
m. (Answer)
and 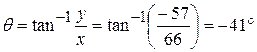 (Answer)
(Answer)
|
(Although 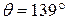 has the same tangent as - 41°, study of the signs of the components of
has the same tangent as - 41°, study of the signs of the components of 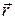 rules out 139°.)
rules out 139°.)
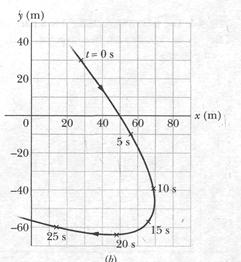
(b) Graph the rabbit's path for 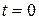 to
to  s.
s.
Solution: We can repeat part (a) for several values of  and then plot the results. Figure 4-36 shows the plots for five values of
and then plot the results. Figure 4-36 shows the plots for five values of  and the path connecting them. We can also use a graphing calculator to make a. parametric graph; that is, we would have the calculator plot ó versus x, where these coordinates are given by Eqs. 4-5 and 4-6 as functions of time
and the path connecting them. We can also use a graphing calculator to make a. parametric graph; that is, we would have the calculator plot ó versus x, where these coordinates are given by Eqs. 4-5 and 4-6 as functions of time  .
.
4-3 Average Velocity and Instantaneous Velocity
If a particle moves through a displacement 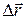 in a time interval
in a time interval 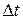 , then its average velocity
, then its average velocity 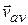 is
is
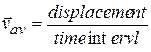 Or
Or 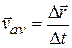 (4-8)
(4-8)
This tells us the direction of 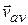 must be the same as that of the displacement
must be the same as that of the displacement 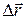 . Using Eq. 4-4, we can write Eq. 4-8 in vector components as
. Using Eq. 4-4, we can write Eq. 4-8 in vector components as
 (4-9)
(4-9)
For example, if the particle in Sample Problem 4-1 moves from its initial position to its later position in 2.0 s, then its average velocity during that move is
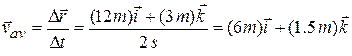
When we speak of the velocity of a particle, we usually mean the particle's instantaneous velocity 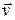 at some instant. This
at some instant. This 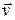 is the value that
is the value that 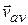 approaches in the limit as we shrink the time interval
approaches in the limit as we shrink the time interval 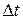 to 0 about that instant. Using the language of calculus, we may write
to 0 about that instant. Using the language of calculus, we may write 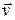 as the derivative
as the derivative
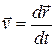 (4-10)
(4-10)
Figure 4-4 shows the path of a particle that is restricted to the  plane. As the particle travels to the right along the curve, its position vector sweeps to the right. During time interval
plane. As the particle travels to the right along the curve, its position vector sweeps to the right. During time interval 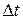 , the position vector changes from
, the position vector changes from 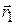 to
to 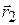 , and the particle's displacement is
, and the particle's displacement is 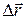 .
.
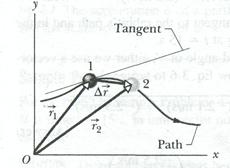 Fig. 4-4
Fig. 4-4
|
To find the instantaneous velocity of the particle at, say, instant 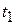 (when the particle is at position 1), we shrink interval
(when the particle is at position 1), we shrink interval 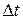 to 0 about
to 0 about 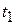 . Three things happen as we do so: (1) Position vector
. Three things happen as we do so: (1) Position vector 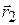 in Fig. 4-4 moves toward
in Fig. 4-4 moves toward 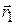 so that
so that 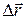 shrinks toward zero. (2) The direction of
shrinks toward zero. (2) The direction of 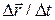 (thus of
(thus of 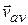 ) approaches the direction of the tangent line to the particle's path at position 1. (3) The average velocity
) approaches the direction of the tangent line to the particle's path at position 1. (3) The average velocity 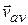 approaches the instantaneous velocity
approaches the instantaneous velocity 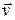 at
at 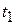 .
.
In the limit as 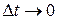 , we have
, we have 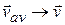 and, most important here,
and, most important here, 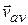 takes on the direction of the tangent line. Thus,
takes on the direction of the tangent line. Thus, 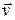 has that direction as well:
has that direction as well:
► The direction of the instantaneous velocity 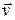 of a particle is always tangent to the particle's path at the particle's position.
of a particle is always tangent to the particle's path at the particle's position.
The result is the same in three dimensions: 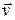 is always tangent to the particle's path.
is always tangent to the particle's path.
To write Eq. 4-10 in unit-vector form, we substitute for 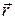 from Eq. 4-1:
from Eq. 4-1:
 .
.
This equation can be simplified somewhat by writing it as
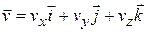 (4-11)
(4-11)
where the scalar components of 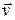 are
are
 (4-12)
(4-12)
For example, 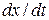 is the scalar component of
is the scalar component of 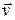 along the
along the  axis. Thus, we can find the scalar components of
axis. Thus, we can find the scalar components of 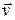 by differentiating the scalar components of
by differentiating the scalar components of 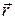 .
.
|
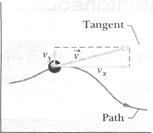
Figure 4-5 shows a velocity vector 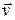 and its scalar x and ó components. Note that
and its scalar x and ó components. Note that 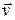 is tangent to the particle's path at the particle's position. Caution: When a position vector is drawn, it is an arrow that extends from one point (a "here") to another point (a "there"). However, when a velocity vector is drawn as in Fig. 4-5, it does not extend from one point to another. Rather, it shows the instantaneous direction of travel of a particle located at the tail, and its length (representing the velocity magnitude) can be drawn to any scale.
is tangent to the particle's path at the particle's position. Caution: When a position vector is drawn, it is an arrow that extends from one point (a "here") to another point (a "there"). However, when a velocity vector is drawn as in Fig. 4-5, it does not extend from one point to another. Rather, it shows the instantaneous direction of travel of a particle located at the tail, and its length (representing the velocity magnitude) can be drawn to any scale.
 Sample Problem 4-3
Sample Problem 4-3
For the rabbit in Sample Problem 4-2, find the velocity 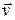 at time
at time 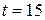 s, in unit-vector notation and as a magnitude and an angle.
s, in unit-vector notation and as a magnitude and an angle.
Solution There are two Key Ideas here: (1) We can find the rabbit's velocity 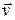 by first finding the velocity components. (2) We can find those components by taking derivatives of the components of the rabbit's position vector. Applying the first of Eqs. 4-12 to Eq. 4-5, we find the x component of
by first finding the velocity components. (2) We can find those components by taking derivatives of the components of the rabbit's position vector. Applying the first of Eqs. 4-12 to Eq. 4-5, we find the x component of 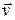 to be
to be
 (4-13)
(4-13)
At 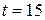 s, this gives
s, this gives 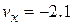 m/s.
m/s.
Similarly, applying the second of Eqs. 4-12 to Eq. 4-6, we find that the 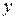 component is
component is
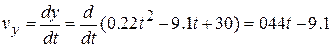
At 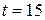 s, this gives
s, this gives 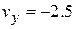 m/s.
m/s.
Equation 4-11 then yields
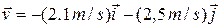 (Answer)
(Answer)
which is shown in Fig. 4-6, tangent to the rabbit's path and in the direction the rabbit is running at 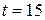 s.
s.
To get the magnitude and angle of 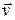 , either we use a vector-capable calculator or we follow Eq. 3-6 to write
, either we use a vector-capable calculator or we follow Eq. 3-6 to write
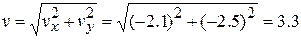 m/s(Answer)
m/s(Answer)
and 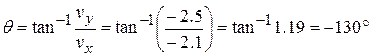 (Answer)
(Answer)
(Although 50° has the same tangent as -130°, inspection of the signs of the velocity components indicates that the desired angle is in the third quadrant, given by 50° - 180° = -130°.)
Date: 2015-01-12; view: 1395
| <== previous page | | | next page ==> |
| Acceleration | | | Average Acceleration and Instantaneous Acceleration |