
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
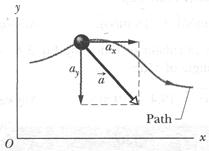
Average Acceleration and Instantaneous Acceleration
When a particle's velocity changes from 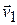 to
to 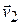 in a time interval
in a time interval 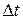 , its average acceleration
, its average acceleration 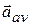 during
during 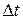 is
is
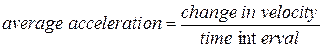
Or
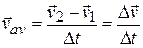
If we shrink 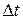 to zero about some instant, then in the limit
to zero about some instant, then in the limit 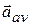 approaches the instantaneous acceleration (or acceleration)
approaches the instantaneous acceleration (or acceleration) 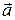 at that instant; that is,
at that instant; that is,
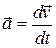 (4-16)
(4-16)
 If the velocity changes in either magnitude or direction (or both), the particle must have an acceleration.
If the velocity changes in either magnitude or direction (or both), the particle must have an acceleration.
We can write Eq. 4-16 in unit-vector form by substituting for v*from Eq. 4-11 to obtain
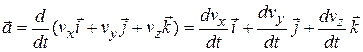
|
We can rewrite this as
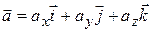 (4-17)
(4-17)
where the scalar components of 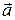 are
are
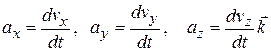 (4-18)
(4-18)
We can rewrite this as
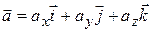 (4-17)
(4-17)
where the scalar components of 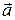 are
are
 ,
, 
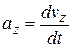 (4-18)
(4-18)
Sample Problem 4-4
For the rabbit in Sample Problems 4-2 and 4-3, find the acceleration 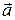 at time
at time 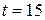 s, in unit-vector notation and as a magnitude and an angle.
s, in unit-vector notation and as a magnitude and an angle.
Solution: There are two Key Ideas here: (1) We can find the rabbit's acceleration 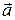 by first finding the acceleration components. (2) We can find those components by taking derivatives of the rabbit's velocity components. Applying the first of Eqs. 4-18 to Eq. 4-13, we find the
by first finding the acceleration components. (2) We can find those components by taking derivatives of the rabbit's velocity components. Applying the first of Eqs. 4-18 to Eq. 4-13, we find the  component of
component of 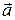 to be
to be
 m/s2
m/s2
Similarly, applying the second of Eqs. 4-18 to Eq. 4-14 yields the 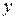 component as
component as
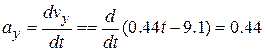 m/s2
m/s2
We see that the acceleration does not vary with time (it is a constant) because the time variable  does not appear in the expression for either acceleration component. Equation 4-17 then yields
does not appear in the expression for either acceleration component. Equation 4-17 then yields
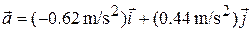 , (Answer)
, (Answer)
which is shown superimposed on the rabbit's path in Fig. 4-8.
To get the magnitude and angle of 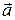 , either we use a vector-capable calculator or we follow Eq. 3-6. For the magnitude we have
, either we use a vector-capable calculator or we follow Eq. 3-6. For the magnitude we have
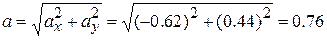 m/s2 (Answer)
m/s2 (Answer)
For the angle we have
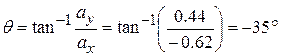
For each description, determine whether the x and ó components of the puck's acceleration are constant, and whether the acceleration a* is constant.

|
However, this last result, which is displayed on a calculator, indicates that 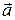 is directed to the right and downward in Fig. 4-8. Yet, we know from the components above that
is directed to the right and downward in Fig. 4-8. Yet, we know from the components above that 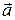 must be directed to the left and upward. To find the other angle that has the same tangent as - 35°, but which is not displayed on a calculator, we add 180°:
must be directed to the left and upward. To find the other angle that has the same tangent as - 35°, but which is not displayed on a calculator, we add 180°:
-35° + 180° = 145c
This is consistent with the components of 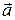 . Note that
. Note that 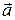 has the same magnitude and direction throughout the rabbit's run because, as we noted previously, the acceleration is constant.
has the same magnitude and direction throughout the rabbit's run because, as we noted previously, the acceleration is constant.
Exercises
1. The position of an object moving only an  -axis is given by
-axis is given by 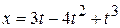 , where
, where  is in meters and
is in meters and  in seconds. (a) What is the position of the object at
in seconds. (a) What is the position of the object at 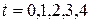 s? (b) What is the displacement’s between
s? (b) What is the displacement’s between 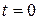 and
and 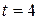 s? (c) What is the average velocity for the time interval from
s? (c) What is the average velocity for the time interval from 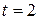 and
and 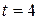 ?
?
2. (a) If particle’s position is given by 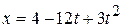 , (where
, (where  is in meters and
is in meters and  in seconds), what its velocity at
in seconds), what its velocity at 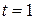 ? (b) Is it moving in positive or negative direction of
? (b) Is it moving in positive or negative direction of  just then? (c) What is its speed just then? (d) Is the speed larger or smaller at later time? (e) Is there ever an instant when the velocity is zero? (f) Is there a time after
just then? (c) What is its speed just then? (d) Is the speed larger or smaller at later time? (e) Is there ever an instant when the velocity is zero? (f) Is there a time after 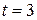 when the particle is moving in the negative direction of
when the particle is moving in the negative direction of  ?
?
3. The position of a particle moving along the  axis is given in centimeters by
axis is given in centimeters by 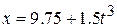 , where
, where  is in seconds. Calculate (a) the average velocity during the time interval
is in seconds. Calculate (a) the average velocity during the time interval 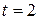 s to
s to 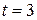 s; (b) the instantaneous velocity at
s; (b) the instantaneous velocity at 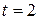 s; (c) the instantaneous velocity at
s; (c) the instantaneous velocity at 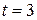 s; (d) the instantaneous velocity at
s; (d) the instantaneous velocity at  s; and (e) the instantaneous velocity when the particle is midway between its positions at f
s; and (e) the instantaneous velocity when the particle is midway between its positions at f 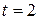 s and
s and 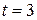 s. (f) Graph
s. (f) Graph  versus
versus  and indicate your answers graphically.
and indicate your answers graphically.
4. A proton moves along the  axis according to the equation
axis according to the equation 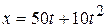 , where
, where  is in meters and
is in meters and  is in seconds. Calculate (a) average velocity of the proton during the first 3.0 s of its motion. (b) the instantaneous velocity of the proton at
is in seconds. Calculate (a) average velocity of the proton during the first 3.0 s of its motion. (b) the instantaneous velocity of the proton at 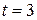 s, (c) the instantaneous acceleration of the proton at
s, (c) the instantaneous acceleration of the proton at 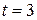 s.
s.
5. An electron moving along the  axis has a position given by
axis has a position given by 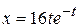 m. where
m. where  is in seconds. How far is the electron from the origin when it momentarily stops?
is in seconds. How far is the electron from the origin when it momentarily stops?
6. The position of a particle moving along the  axis depends on the time according to the equation
axis depends on the time according to the equation 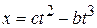 , where
, where  is in meters and
is in meters and  in seconds, (a) What units must ñ and b have? Let there numerical values be 3.0 and 2.0, respectively. (b) At what time does the particle reach its maximum positive
in seconds, (a) What units must ñ and b have? Let there numerical values be 3.0 and 2.0, respectively. (b) At what time does the particle reach its maximum positive  position? From
position? From 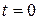 and
and 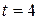 , (c) what distance does the particle move and (d) what is its displacement? At
, (c) what distance does the particle move and (d) what is its displacement? At 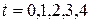 s what are (e) its velocity and (f) its acceleration?
s what are (e) its velocity and (f) its acceleration?
Exercises
The  and
and 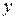 coordinates of a particle at any time
coordinates of a particle at any time  are given by
are given by 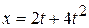 and
and 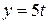 , where
, where  and
and 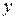 are in meters and
are in meters and  in seconds. The acceleration of the particle at
in seconds. The acceleration of the particle at 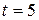 s is
s is
(A) zero (B) 8 m/ s2 (C) 20 m/s2 (D) 40 m·s2
2-34 A jet-propelled motorcycle starts from rest, moves in a straight line with constant acceleration, and covers a distance of 64 m in 4 s.
a)What is the final velocity?
b)How much time was required to cover half the total distance?
c) What is the distance covered in one-half the total time?
d)What is the velocity when half the total distance has been covered?
e) What is the velocity after one-half the total time?
f) When will the instantaneous velocity equal the average velocitv for the 0-to-4 s time interval?
Q. 2.09. If the displacement of a body is proportional to square of time, state whether the body is moving with uniform velocity or uniform acceleration.
Q. 2.10. If the distance traveled by a body in time  is given by
is given by 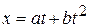 , then what will be the acceleration of the body?
, then what will be the acceleration of the body?
Q. 2.11. An object is covering distance in direct proportion to 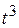 , where
, where  is the time elapsed.
is the time elapsed.
(a) What conclusions might you draw about acceleration? Is it constant? Increasing? Decreasing?
(b) What might you conclude about the force acting on the object?
2. The position of a particle is given by 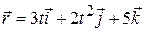 , where t is in seconds and the coefficients have the proper units for
, where t is in seconds and the coefficients have the proper units for 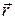 to be in meters.
to be in meters.
(a) Find  and
and 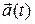 of the particle.
of the particle.
(b) Find the magnitude and direction of  at
at 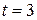 s.
s.
[Ans. (a) 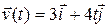 ;
; 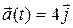 ; (b) 12.37 m/s; 76°]
; (b) 12.37 m/s; 76°]
Section 2—5 Velocity and Coordinate by Integration
2-20 The motion of a particle along a straight line is described by the function
x = (6 m) + (5 m-s-2)/2 - (1 m-s-4)/4.
Assume that t is positive.
a) Find the position, velocity, and acceleration at time t = 2 s.
b)During what time interval is the velocity positive?
c) During what time interval is x positive?
d)What is the maximum positive velocity attained by the particle?
2—21 The acceleration of a motorcycle is given by a - (1.2 m-s-3)/ - (0.12 m-s-4)/2. It is at rest at the origin
at time t — 0.
Find its position and velocity as functions of time.
a) Calculate the maximum velocity it attains.
2-22 The acceleration of a bus is given by a = (2 m-s-3)t.
) If the bus's velocity at time t = 1 s is 5 m-s-1, what is its velocity at time ( = 2s?
b) If the bus's position at time t = 1 s is 6 m, what is its position at time t = 2 s?
56 The acceleration of an object suspended from a spring and oscillating vertically is 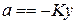 , where
, where 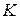 is a constant and
is a constant and 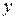 is the coordinate measured from the equilibrium position. Suppose that an object moving in this way is given an initial velocity
is the coordinate measured from the equilibrium position. Suppose that an object moving in this way is given an initial velocity 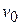 at the coordinate
at the coordinate 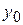 . Find the expression for the velocity
. Find the expression for the velocity 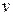 of the object as a function of its coordinate
of the object as a function of its coordinate 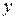 .
.
2-57 The motion of an object falling from rest in a resisting medium is described by the equation

where A and  are constants. In terms of A and B, find
a) the initial acceleration;
b) the velocity at which the acceleration becomes zero (the terminal velocity).
c) Show that the velocity at any given t is given by
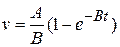
2-58 After the engine of a moving motorboat is cut off, the boat has an acceleration in the opposite direction to its velocity and directly proportional to the square of its velocity. That is,  , where
, where 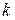 is constant.
is constant.
a) Show that the magnitude 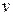 of the velocity at a time
of the velocity at a time  after the engine is cut off is given by
after the engine is cut off is given by
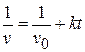 .
.
b) Show that the distance x traveled in a time  is
is
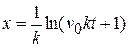
c) Show that the velocity after traveling a distance  is
is
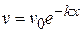
As a numerical example, suppose the engine is cut off when the velocity is 6 m/s, and that the velocity decreases to 3 m/s in a time of 15 s.
d) Find the numerical value of the constant 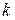 , and the unit in which it is expressed.
, and the unit in which it is expressed.
e) Find the acceleration at the instant the engine is cut off.
f) Calculate x, v, and a at 10-s intervals for the first 60 s after the engine is cut off. Sketch graphs of x, v. and a as
functions oi t, tor the first 60 s of the motion.
Date: 2015-01-12; view: 3705
| <== previous page | | | next page ==> |
| Motion in Two or Three Dimensions | | | Uniform Circular Motion |