Acceleration

When a particle's velocity changes, the particle is said to undergo acceleration (or to accelerate). For motion along an axis, the average acceleration 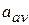over a time interval 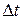is

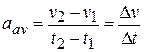(1-7)

where the particle has velocity at time 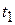and then velocity 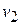at time 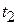. The instantaneous acceleration (or simply acceleration) is the derivative of the velocity with respect to time:

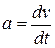(1-8)

In words, the acceleration of a particle at any instant is the rate at which its velocity is changing at that instant. Graphically, the acceleration at any point is the slope of the curve of at that point.

We can combine Eq. 1-8 with Eq. 1-4 to write

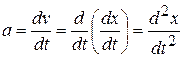(1-9)

In words, the acceleration of a particle at any instant is the second derivative of its position 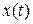with respect to time.

A common unit of acceleration is the meter per second per second: m/(s • s) or m/s². You will see other units in the problems, but they will each be in the form of length/(time • time) or length/time². Acceleration has both magnitude and direction (it is yet another vector quantity). Its algebraic sign represents its direction on an axis just as for displacement and velocity; that is, acceleration with a positive value is in the positive direction of an axis, and acceleration with a When is constant, the derivative is zero and so also is the acceleration.

Your body reacts to accelerations (it is an accelerometer) but not to velocities (it is not a speedometer). When you are in a car traveling at 90 km/h or an airplane traveling at 900 km/h, you have no bodily awareness of the motion. However, if the car or plane quickly changes velocity, you may become keenly aware of the change, perhaps even frightened by it.

Large accelerations are sometimes expressed in terms of units, with

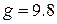m/s²

Example 1-4

A particle's position on the axis of Fig. 1-1 is given by

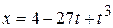, with in meters and in seconds.

a) Find the particle's velocity function 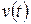and acceleration function .

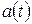Solution. One Key Idea is that to get the velocity function 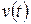, we differentiate the position function 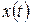with respect to time. Here we find

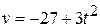
with in meters per second.

Another Key Idea is that to get the acceleration function 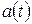, we differentiate the velocity function 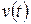with respect to time. This gives us

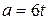, (Answer)

with 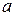in meters per second squared.

(b) Is there ever a time when ?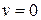

Solution. Setting 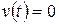yields

0 = -27 + 3t², which has the solution

t = ±3 s. (Answer)

Thus, the velocity is zero both 3 s before and 3 s after the clock reads 0.

(c) Describe the particle's motion for .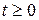

Solution. The Key Idea is to examine the expressions for 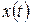, , 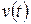and .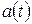

At 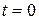, the particle is at 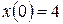m and is moving with a velocity of 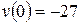m/s - that is, in the negative direction of the axis. Its acceleration is 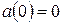, because just then the particle's velocity is not changing.

For 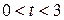s, the particle still has a negative velocity, so it continues to move in the negative direction. However, its acceleration is no longer 0 but is increasing and positive. Because the signs of the velocity and the acceleration are opposite, the particle must be slowing.

Indeed, we already know that it stops momentarily at 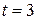s. Just then the particle is as far to the left of the origin in Fig. 2-1 as it will ever get. Substituting 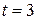s into the expression for 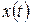, we find that the particle's position just then is 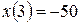m. Its acceleration is still positive.

For 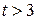s, the particle moves to the right on the axis. Its acceleration remains positive and grows progressively larger in magnitude. The velocity is now positive, and it too grows progressively larger in magnitude.

Exercises

1.33 A motorcycle's position is described by 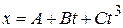x = A + Bt + Ct^s, where A, B, and С are numerical constants.

a)Calculate the velocity of the cycle, as a function of time.

b) From your answer to (a), calculate the acceleration of the motorcycle as a function of time.

1.. Are rest and motion absolute or relative terms

1.02. Under what condition will the distance and displacement of a moving object will have the same magnitude?

1..03. What will be nature of graph for a uniform motion?

1.04. Can graph be a straight line parallel to time-axis?

1.05. Can graph be a straight line parallel to position-axis?

1.06. What does slope of 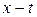graph represent?

1.07. Can 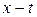graph have a negative slope?

1..08. Can a particle in one dimensional motion with zero speed may have non-zero velocity

1..09. Can a body have a constant velocity but a varying speed?

1..10. Can a body have a constant speed but a varying velocity? Or Is it possible for a body to be accelerated, if its speed is constant ? If it is so, give an example.

Ans. Yes. When a body moves along a circular path with/ uniform angular speed, it possesses constant speed but a varying velocity.

1..11. What does the speedometer of a car measure?

1..12. When will the relative velocity of two moving objects be zero?

1..06 Is magnitude of the displacement of an object and the total distance covered by it in certain time interval same? Explain.

1. A cyclist moves along a circular path of radius 70 m. If he completes one round in 11 s, calculate (i) total length of path, (ii) magnitude of the displacement, (iii) average speed and (iv) magnitude of average velocity.

[Ans. (i) 440 m ; (it) zero ; (iii) 40 m s^_1; (iv) zero]

Date: 2015-01-12; view: 1074