Instantaneous Velocity and Speed

You have now seen two ways to describe how fast something moves: average velocity and average speed, both of which are measured over a time interval 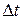. However, the phrase "how fast" more commonly refers to how fast a particle is moving at a given instant - and that is its instantaneous velocity (or simply velocity) .

The velocity at any instant is obtained from the average velocity by shrinking the time interval 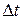closer and closer to 0. As 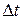dwindles, the average velocity approaches a limiting value, which is the velocity at that instant:

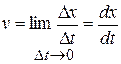(1-4)

This equation displays two features of the instantaneous velocity . First, is the rate at which the particle's position is changing with time at a given instant; that is, is the derivative of with respect to . Second, at any instant is the slope of the particle's position-time curve at the point representing that instant. Velocity is another vector quantity and thus has an associated direction.

Speed is the magnitude of velocity; that is, speed is velocity that has been stripped of any indication of direction, either in words or via an algebraic sign. A velocity of +5 m/s and one of -5 m/s both have an associated speed of 5 m/s. The speedometer in a car measures the speed, not the velocity, because it cannot determine the direction.

Example 2-3

The position of a particle moving on an axis is given by

with in meters and in seconds. What is its velocity at 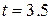s? Is the velocity constant, or is it continuously changing?

Solution. For simplicity, the units have been omitted from Eq. 1-5, but you can insert them if you like by changing the coefficients to 7.8 m, 9.2 m/s, and -2.1 m/s³. The Key Idea here is that velocity is the first derivative (with respect to time) of the position function 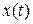. Thus, we write

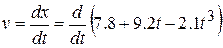
which becomes

1-6 (Answer)

At 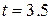s, the particle is moving in the negative direction of (note the minus sign) with a speed of 68 m/s. Since the quantity appears in Eq. 1-6, the velocity depends on and so is continuously changing.

Exercises

1.5 A hobbyist is testing a new model rocket engine by using it to propel a cart along a model railroad track. He determines that its motion along the -axis is described by the equation 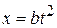, where = 10 cm/s². Compute the instantaneous velocity of the cart at time 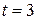s.

1.6 A car is initially stopped at a traffic light. It then travels along a straight road such that its distance from the light is given by 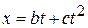, where b= 4.0 m/s and с = 0.5 m/s².

a) Calculate the average velocity of the car for the time interval = 0to =10s.

b)Calculate the instantaneous velocity of the car at i) t =0; ii) t = 5 s; iii) t =10 s

Date: 2015-01-12; view: 1114