Kinematics

Our study of physics begins in the area of mechanics, which deals with the relations among force, matter, and motion. Mechanics consists of: kinematics, dynamics and static.

Kinematics is the study of motion of objects without taking into account the causes of their motion.

Dynamics is the study of motion of objects by taking into account the cause of their change of state (rest or of uniform motion).

Static is study of the object at rest under the effect of forces in equilibrium.

Motion is a continuous change of the position of a body with respect to its surroundings

In physics we are concerned with three types of motion: translational, rotational, and vibrational. A car moving down a highway is an example of translational motion, the Earth's spin on its axis is an example of rotational motion, and the back-and-forth movement of a pendulum is an example of vibrational motion.

In our study of translational motion, we describe the moving object as a particle regardless of its size. In general a particle is a point-like mass having infinitesimal size. For example, if we wish to describe the motion of the Earth around the Sun, we can treat the Earth as a particle and obtain reasonably accurate data about its orbit. We say that the particle is a model for a moving body; it provides a simplified, idealized description of the position and motion of the body.

1-1 Position and Displacement

To locate an object means to find its position relative to some reference point, often the origin (or zero point) of an axis such as the axis in Fig. 2-1. The positive direction of the axis is in the direction of increasing numbers (coordinates), which is toward the right in Fig. 1. The opposite direction is the negative direction.

Fig. 1-1

For example, a particle might be located at 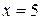m, which means that it is 5 m in the positive direction from the origin. If it were at 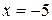m, it would be just as far from the origin but in the opposite direction.

A change from one position to another position is called a displacement 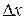, where

(1)

(The symbol , the Greek uppercase delta, represents a change in a quantity, and it means the final value of that quantity minus the initial value.) When numbers are inserted for the position values and , a displacement in the positive direction (toward the right in Fig. 1) always comes out positive, and one in the opposite direction (left in the figure), negative. For example, if the particle moves from = 5m to = 12 m, then . The positive result indicates that the motion is in the positive direction. If the particle then returns to 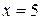m, the displacement for the full trip is zero. The actual number of meters covered for the full trip is irrelevant; displacement involves only the original and final positions.

A plus sign for a displacement need not be shown, but a minus sign must always be shown. If we ignore the sign (and thus the direction) of a displacement, we are left with the magnitude (or absolute value) of the displacement. In the previous example, the magnitude of 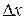is 7 m.

Displacement is an example of a vector quantity, which is a quantity that has both a direction and a magnitude. Here all we need is the idea that displacement has two features: (1) Its magnitude is the distance (such as the number of meters) between the original and final positions. (2) Its direction, from an original position to a final position, can be represented by a plus sign or a minus sign if the motion is along a single axis.

•CHECKPOINT 1: Here are three pairs of initial and final positions, respectively, along an axis. Which pairs give a negative displacement: (a) ; (b) ; (c) ?

Exercises

1. A watermelon seed has the following coordinates: m, m, and m. Find its position vector (a) in unit-vector notation and as (b) a magnitude and (c) an angle relative to the positive direction of the axis, (d) Sketch the vector on a right-handed coordinate system. If the seed is moved to the xyz coordinates (3.00 m, 0 m, 0 m), what is its displacement (e) in unit-vector notation and as (f) a magnitude and (g) an angle relative to the positive direction of the x axis?

2. The position vector for an electron is . (a) Find the magnitude of 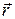. (b) Sketch the vector on a right-handed coordinate system.

3, The position vector for a proton is initially 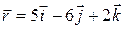and then later is 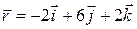, all in meters. (a) What is the proton's displacement vector, and (b) to what plane is that vector parallel?

1-2 Average Velocity and Average Speed

A compact way to describe position is with a graph of position plotted as a function of time - a graph of 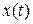. (The notation 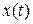represents a function

Fig. 1-2

of , not the product times .) As a simple example, Fig. 1-2 shows the position function 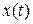for a stationary armadillo (which we treat as a particle) at m.

Fig.2-2. The graph of 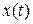for an armadillo that is stationary at m. The value of is 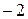m for all times

Figure 1-3a, b

Figure 1-3a, also for an armadillo, is more interesting, because it involves motion. The armadillo is apparently first noticed at 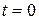when it is at the position 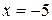m. It moves toward 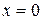, passes through that point at 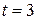s, and then moves on to increasingly larger positive values of .

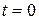Figure 1-3b depicts the actual straight-line motion of the armadillo and is something like what you would see. The graph in Fig. 1-3a is more abstract and quite unlike what you would see, but it is richer in information. It also reveals how fast the armadillo moves.

Actually, several quantities are associated with the phrase "how fast." One of them is the average velocity 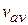, which is the ratio of the displacement 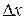: that occurs during a particular time interval 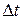to that interval^

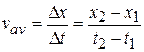(1-2)

The notation means that the position is at time 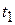and then at time 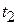. A common unit for 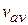is the meter per second (m/s). You may see other units in the problems, but they are always in the form of length/time.

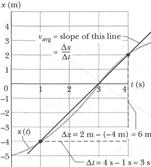Figure 1-4

On a graph of versus , 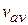is the slope of the straight line that connects two particular points on the 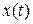curve: one is the point that corresponds to and 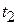, and the other is the point that corresponds to and 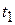. Like displacement, 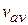has both magnitude and direction (it is another vector quantity). Its magnitude is the magnitude of the line's slope. A positive 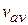(and slope) tells us that the line slants upward to the right; a negative 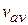(and slope), that the line slants downward to the right. The average velocity 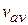always has the same sign as the displacement 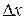because 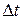in Eq. 1-2 is always positive. Figure 1-4 shows how to find 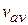for the armadillo of Fig. 1-3, for the time interval 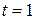s to 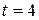s. We draw the straight line that connects the point on the position curve at the beginning of the interval and the point on the curve at the end of the interval. Then we find the slope 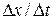of the straight line. For the given time interval, the average velocity is

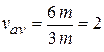m/s.

Average speed is a different way of describing "how fast" a particle moves. Whereas the average velocity involves the particle's displacement 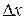, the average speed involves the total distance covered (for example, the number of meters moved), independent of direction; that is,

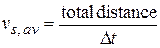
Because average speed does not include direction, it lacks any algebraic sign. Sometimes is the same (except for the absence of a sign) as 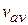. However, as is demonstrated in Sample Problem 1-1, when an object doubles back on its path, the two can be quite different.

Example 1-1

You drive a beat-up pickup truck along a straight road for 8.4 km at 70 km/h, at which point the truck runs out of gasoline and stops. Over the next 30 min, you walk another 2.0 km farther along the road to a gasoline station.

(a) What is your overall displacement from the beginning of your
drive to your arrival at the station?

Solution. Assume, for convenience, that you move in the positive direction of an axis, from a first position of to a second position of at the station. That second position must be at 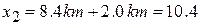km. Then your displacement 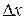along the axis is the second position minus the first position. From Eq. 1-1, we have

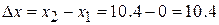km. (Answer)

Thus, your overall displacement is 10.4 km in the positive direction of the axis.

(b) What is the time interval 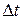from the beginning of your drive
to your arrival at the station?

Solution. We already know the time interval 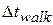(= 0.50 h) for the walk, but we lack the time interval 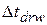for the drive. However, we know that for the drive the displacement is 8.4 km and the average velocity 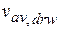is 70 km/h. A Key Idea to use here comes from Eq. 1-2: This average velocity is the ratio of the displacement for the drive to the time interval for the drive:

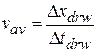
Rearranging and substituting data then give us

h.

So, 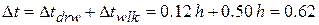h. (Answer)

(c) What is your average velocity 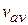from the beginning of your drive to your arrival at the station? Find it both numerically and graphically.

Solution. The Key Idea here again comes from Eq. 1-2: 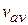for the entire trip is the ratio of the displacement of 10.4 km for the entire trip to the time interval of 0.62 h for the entire trip. With Eq. 1-2, we find it is

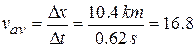km/h (Answer)

To find 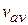graphically, first we graph 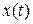as shown in Fig. 1-5, where the beginning and arrival points on the graph are the origin and the point labeled as "Station." The Key Idea here is that your average velocity is the slope of the straight line connecting those points; that is, it is the ratio of the rise ( 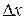= 10.4 km) to the run ( 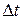= 0.62 h), which gives us 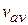= 16.8 km/h.

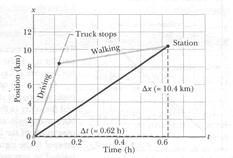Fig. 1-5

(d) Suppose that to pump the gasoline, pay for it, and walk back to the truck takes you another 45 min. What is your average speed from the beginning of your drive to your return to the truck with the gasoline?

Solution.: The Key Idea here is that your average speed is the ratio of the total distance you move to the total time interval you take to make that move. The total distance is 8.4 km + 2.0 km + 2.0 km = 12.4 km. The total time interval is 0.12 h + 0.50 h + 0.75 h = 1.37 h. Thus, Eq. 2-3 gives us

km/h (Answer)

Date: 2015-01-12; view: 1132