
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
DYNAMICS OF ROTATIONAL MOTION. DETERMINATION OF LOADS INERTIA MOMENT USING OBERBECH’S PENDULUM
| The purpose of the work. to study the basic rotational motion dynamics law; to determine the rotating solid body inertia moment. | Devices and accessories 1. Pendulum. 2. Set of loads. 3. Electronic stop-watch. 4. Ruler. |
Task 1. Determination of inertia moment of Oberbech’s pendulum crosspiece.
1.1. Remove loads from the rods.
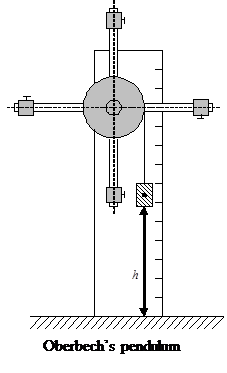 1.2. Measure the diameter of pulley with trammel. Write down the result as:
1.2. Measure the diameter of pulley with trammel. Write down the result as:
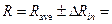 __________________ m,
__________________ m,
where DRin is instrumental error of radius determination.
1.3. Write down the value of falling load mass and height, the load falls from:
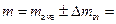 __________________ kg,
__________________ kg,
 __________________ m,
__________________ m,
where 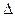 m is an instrumental error of mass measurement; Dh is an instrumental error of height measurement.
m is an instrumental error of mass measurement; Dh is an instrumental error of height measurement.
1.4. Let the load go down and measure the time of its falling down to a lower score with a stop watch. Repeat measurement 5 times and enter the results into table 1.
Task 2. Determination of inertia moment of Oberbech’s pendulum with loads
2.1. Fix loads at the first rods scores near the pulley and carry out measurements according to item 1.4.
2.2. Determine the distance between the centre of rotating loads and the centre of pendulum rotation. Enter the result into table 1.
2.3. Fix loads on a medial, and then on farthest scores of the rods and repeat measurements according to items 1.4 and 2.2. Enter the obtained result into table 1.
2.4. Determine random error of falling load time measurement for position without loads:
— calculate average values 
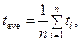
where n = 5 is amount of measurement;
— calculate the deviation of the measured values of time from it mean value 
— determine the root-mean-square error:
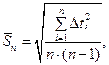
— calculate the absolute error of falling load time measurement:
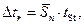
where the Student’s coefficient is tSt = 2,78 (n = 5 and a = 0,95);
— determine the absolute error according to the formula:
Dt = 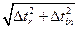 ,
,
— determine the fractional error according to the formula:
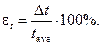
Enter the results into table 2.
Table 1
| Position | Exp. No | Time of the load falling down, t, s | Average value of time, 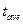 , s , s
| Pulley radius, R, m | Distance from the center of rotation to the load center 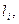 m m
| Height, the load falls from h, m | Mass of the falling load, m, kg |
| Without loads | |||||||
| ˛ | |||||||
| ˛˛ | |||||||
| ˛˛˛ | |||||||
Table 2
| Position | Exp. No | Average value tave, s | Deviation from mean value 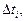 s s
| Root-mean-square deviation 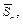 s s
| Absolute error Dt, s | Fractional error et, % |
| Without loads | ||||||
Task 3. Determination of inertia moments of the loads in three positions
3.1. Calculate the moments of inertia of pendulum without loads 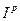 and with loads in positions I, II and III:
and with loads in positions I, II and III: 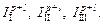
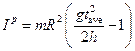 = kg×m2,
= kg×m2,
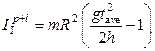 = kg×m2,
= kg×m2,
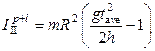 = kg×m2,
= kg×m2,
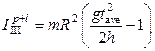 = kg×m2.
= kg×m2.
Enter the results into table 3.
3.2. Calculate the fractional error of the inertia moment of pendulum 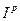 measurement using formula:
measurement using formula:
ep = 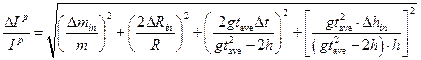 =
=
=_______________________________________________________________________________
where Dmin, Dhin, DRin are instrumental errors of load mass, height and pulley radius measurements; Dt is absolute error of load falling down time measurement.
3.3. Calculate the absolute error of 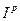 determination using formula:
determination using formula:
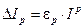 =______________________________________________ kg×m2.
=______________________________________________ kg×m2.
Task 4. Graph plotting.
Plot the graph as the dependence of loads inertia moment upon the square of loads distance to the rotation centre.
4.1. Calculate inertia moments of the loads in three positions.
 kg×m2,
kg×m2,
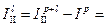 kg×m2,
kg×m2,
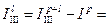 kg×m2.
kg×m2.
Enter the results into table 3.
Table 3
| Position | Distance from the center of rotation to the load center 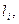 m m
| Moment of inertia, I, kg · m2 |
 , m2 , m2
| ||
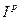
| 
| 
| |||
| ithout loads | |||||
| I | |||||
| II | |||||
| III |
4.2. Plot the graph as the dependence of loads inertia moment upon the square of loads distance to the rotation centre, using data from Table 3.

Conclusions
The data of laboratory work fulfillment
Pass mark Signature
Mark of laboratory work defending Signature
questions to be admitted for doing laboratory work and its defending
1. Give the definition of rotational motion.
2. Name kinematic characteristics of rotational motion
3. Name dynamic characteristics of rotational motion.
4. What is moment of force (torque)? What does moment of force depend on? Formulate the rule of determination of torque direction.
5. What is angular momentum? What does angular moment depend on?
6. What is inertia moment? What are the equations applied for determination of inertia moment of material point and rigid body?
7. Formulate Steiner’s theorem and explain its application.
8. Formulate basic dynamics laws for translational motion of material point and rigid body.
9. Formulate basic dynamics laws for rotational motion of material point and rigid body.
10. Formulate the angular momentum conservation law.
11. Deduce the expression for calculation of moment of inertia.
12. Formulate the main stages of laboratory work fulfillment.
LABORATORY WORK
Date: 2015-01-12; view: 1622
| <== previous page | | | next page ==> |
| THE PHYSICAL MEASUREMENT ERRORS CALCULATION | | | DETERMINATION OF LIQUID VISCOSITY COEFFICIENT |