
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
THE PHYSICAL MEASUREMENT ERRORS CALCULATION
Determination of a Solid Body Density
| The purpose of the work: to study the rules of physical measurement results treatment; to determine the error of the indirect measurements of the cylindrical body density as a result of the repeated direct measurements of its geometrical values and mass | Devices and accessories 1. Cylinder standard. 2. Ruler. 3. Slide-clipper. 4. Micrometer. |
Task 1. Measurement of cylindrical body parameters
1.1. Measure diameter d and height h of the cylindrical body by using slide-clipper and micrometer. Repeat all measurements 5 times. Enter the obtained results into table 1.
Table 1
| Experiment number | Measured value | Average value | Deviation of measured value from average value | Root-mean-square error | Instrumental error | Random absolute error | Absolute error of direct measurements | Fractional error |
| Mass of sample, m, g | ||||||||
| Exp. No | mi | 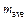
|  g g
| 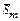
| 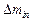 , g , g
| 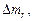 g g
|  , g , g
| 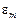 , % , %
|
| Diameter of sample, d, mm | ||||||||
| Exp. No | di | 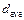
| 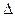  mm mm
| 
| 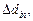 mm mm
| 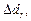 mm mm
| 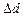 , mm , mm
| 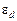 , % , %
|
| Height of sample, h, mm | ||||||||
| Exp. No | hi | 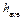
| 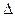  mm mm
| 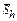
| 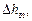 mm mm
| 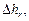 mm mm
|  , mm , mm
| 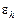 , % , %
|
1.2. Take values of sample mass from a teacher. Enter the obtained results into table 1.
1.3. Enter instrumental errors of mass, diameter and height measurements into table 1.
Task 2. Determination of direct measurements absolute error. Algorithm for calculation.
2.1. Determine an arithmetic mean value of all measurement results according to the formula:
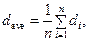
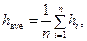
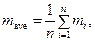
where n = 5 is amount of measurements. Enter the obtained data into table 1.
2.2. Calculate random deviation of every obtained result according to the formula:


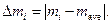
2.3. Determine root-mean-square deviations according to the formula:
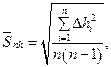
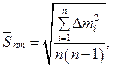

Enter the obtained data into table 1.
2.4. Determine random errors of direct measurements according to the formula:

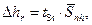
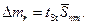
where the Studentís coefficient is tSt = 2,78 (n = 5 and a = 0,95).
Calculations are performed with the accuracy of three or four significant digits. Enter the obtained data into table 1.
2.5. Determine an absolute error according to the formula:
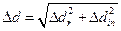 ;
;  ;
; 
Enter the obtained data into table 2.
2.6. Determine the fractional error of measurements results according to the formula:
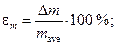
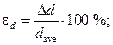
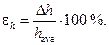
2.7. Calculate the resulting fractional error for density of a body according to the formula:

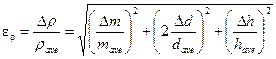 =
=
=______________________________________________________________________
Task 3. Calculation of the body density and absolute error of indirect measurement
3.1. Calculate average value of a body density 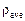 in SI units by using values
in SI units by using values 
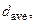
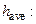

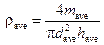 =
= 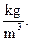
3.2. Calculate the absolute error of the body density measurement according to the formula:
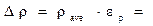 __________________________
__________________________ 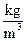 .
.
3.3. Write down the final result in the following form:
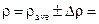 ___________________________
___________________________ 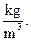
3.4. Calculate the fractional error of the cylindrical body density measurement according to the formula:
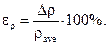
Determine the material the cylindrical body made of using table 2. Table 2
| Material | Density, 103 kg/m3 | Material | Density, 103 kg/m3 |
| Oak | 0,8 | Iron (steel) | 7,8 |
| Graphite | 1,6 | Brass | 8,4 |
| Aluminum | 2,7 | Copper | 8,9 |
| Zinc | 7,1 | Molybdenum | 10,2 |
| Tin | 7,4 | Lead | 11,3 |
Conclusions
As a result of laboratory work fulfillment the body density was determined:
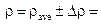
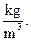
According to the obtained results the material the cylinder body made of is:
Fractional error of measurements is 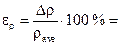
The data of laboratory work fulfillment
Pass mark Signature
Mark of laboratory work defending Signature
questions to be admitted for doing laboratory work and its defending
1. Give the definition of physical quantity measurement.
2. Give the definition of measure.
3. Give the definition of a measuring device.
4. Give the definition of a measurement error.
5. Give the definition of absolute and fractional errors of measurements.
6. What is measurement accuracy?
7. Give the definition of the direct measurement. Give an example.
8. Give the definition of the indirect measurement. Give an example.
9. Give the definition of systematic error. What types of systematic errors do you know?
10. Characterize the methodical systematic error.
11. Characterize the instrumental systematic error.
12. Characterize the personal systematic error.
13. Define and characterize the random errors.
14. Give the direct measurements error estimation rules.
15. How can random and systematic errors be taken into account?
16. Define and characterize gross (rough) errors.
LABORATORY WORK
Date: 2015-01-12; view: 1943
| <== previous page | | | next page ==> |
| Experimental equipment | | | DYNAMICS OF ROTATIONAL MOTION. DETERMINATION OF LOADS INERTIA MOMENT USING OBERBECHíS PENDULUM |