Forced vibrations

If body is displaced from its equilibrium position and then not interfered with, the vibrations occur at the natural frequency of the body, independent of the natural excitation, i.e., the vibrations are determined only by the properties of the system.

At the same time, there exists a number of means of “blocking” the vibrations of a body to an external frequency. Such forced vibrations may take place in two bodies capable of vibrating are coupled. One of the bodies will force the other to vibrate.

Forced vibrations do not set in immediately. A certain amount of time must elapse before the body coupled to the vibrating system begins to vibrate. Eventually, a particular amplitude is reached and the frequency of the vibrations will be exactly equal to 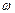. Fig. shows the dependence of the amplitude of forced vibrations on the amplitude of forced vibrations on the ratio ω/ω₀ for three system having different amounts of friction.

When the external frequency and the natural frequency coincide, the amplitude of the forced vibrations is a maximum. This phenomenon is widely known as resonance. The equation of motion of a body executing forced vibrations, under action of a periodic external force 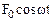has the form

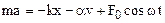(8.50)

By substitution, one can easily show that the displacement of a vibrating point will satisfy the equation

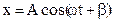(8.51)

where the amplitude

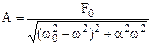(8.52)

and the phase shift 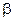satisfies the equation

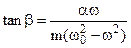(8.53)

From the first formula it follows that the amplitude A depends on 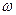as follows:

when 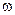< 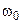the amplitude increases as 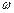increases;

when 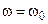the amplitude riches maximum;

when 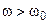the amplitude decreases as 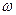increases.

When there is little friction, the resonance disrupts the system, for at the resonance amplitude goes to infinity. A simple experiment will demonstrate the essence of these interesting relationships.

Suspend a weight by a string and allow it to swing freely. When the period of the free vibrations of this pendulum is manifested, stop the pendulum and by periodic motion of the hand bring it into a state of forced vibration. At first move the hand rapidly, so that the period of the forced vibrations; then move it slowly, so that the period of the natural vibrations. It will be seen that in the first case the pendulum and the hand are 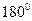out of phase, while in the second case they are in phase.

Date: 2015-01-12; view: 1104