Velocity, Acceleration, Energy of Harmonic Oscillations

Corresponding formulas can easily be deduced. These equations may be derived from

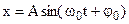. (8.3)

The velocity of harmonic oscillation:

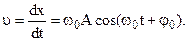(8.4)

The acceleration of harmonic oscillation:

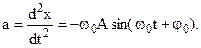(8.5)

The kinetic and potential energy of harmonic oscillation:

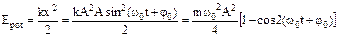_. (8.6)

Consequently total energy:

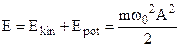(8.7)

and it doesn’t depend upon time. In the process of harmonic oscillations potential energy transforms into the kinetic energy and vise-versa.

Changes in the state of a system when it repeated by returns to the same state after certain time intervals are called periodic processes. A simple illustration of oscillatory motion is the motion of particle m suspended by a string or spring vibrating about position of equilibrium – a point O.

If the body of particle on which forces are acting its in a position of equilibrium, its potential energy is a minimum and the system is in a potential well. When deviation from the equilibrium position is not large, we are concerned with only a small partition of the potential well. A potential curve near the equilibrium position can always be approximated by parabola.

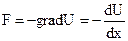(8.8)

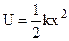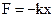, (8.9)

As is well known, making the proper assumptions, any function may be expanded in a Taylor series for small values of x. The exponent of x increases consecutively from term to term

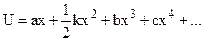; (8.10)

However, for small x, the terms of higher power may be neglected and, if the potential well is symmetrical, the first term vanishes, for the potential energies at equal distances to the left and right of equilibrium are equal. Newton law for the restoring force

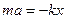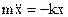, (8.11)

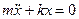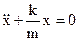; (8.12)

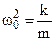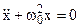; (8.13)

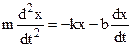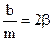; (8.14)

(8.15)

The equation of motion

(8.16)

For time dt the lose of energy is

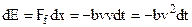(8.17)

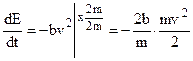(8.18)

So as the average kinetic energy is equal half energy for the vibration motion, then

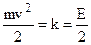(8.19)

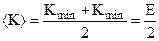(8.20)

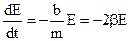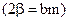, (8.21)

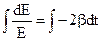(8.22)

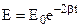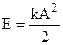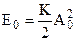, ; (8.23)

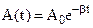(8.24)

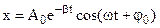(8.25)

This equation is satisfied if the point undergoes harmonic vibration about the equilibrium position

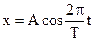(8.26)

where T is the period of vibration. Let us verify this statement

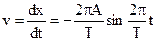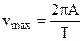; (8.27)

(8.28)

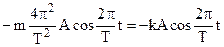(8.29)

As can be seen from the last formula, the period of the free vibrations about the equilibrium position is

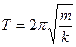(8.30)

This period is called the natural or characteristics period of the vibrating system. If there is no friction, the total energy ε of a body naturally remains unchanged for vibrations about its equilibrium position. At any instant of motion

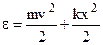(8.31)

Friction produces damped vibrations. The equation of motion is written as follows

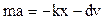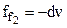, (8.32)

where coefficient α is the resistance constant

(8.33)

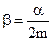(8.34)

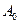is the amplitude at the instant of time t = 0. The expressions for the amplitude after n-1 and n periods, respectively, are

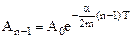and 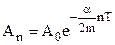(8.35)

Let us divide the former relation by latter. The ratio

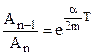(8.36)

does not, in fact, depend on n. The rate of damping is sometimes expressed by the logarithmic decrement

(8.37)

The same calculation that leads to the formula for the time dependence of the amplitude of the amplitude also yields the following relation for the period

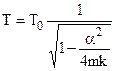(8.38)

This means that, for small resistance, T differs little from

(8.39)

Let us examine the system, shown in fig. If we take the vessel away the body m will perform harmonic oscillations whose frequency we denote by 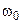. 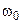is defined by the coefficient of elasticity of the spring k and mass of the oscillator body m, thus

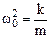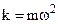; (8.40)

In the presence of friction the motion retards, owing to this the period of oscillation increases, and the frequency of oscillation increases, and the frequency of oscillations decreases. In this case the oscillating body is under the action of two forces: restoring force on the part of the spring

(8.41)

and the force of friction

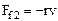, (8.42)

where r is a coefficient of friction; v is velocity. Applying Newton’s second law we obtain.

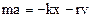(8.43)

Let us consider oscillatory motion described by the formula.

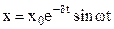(8.44)

The value 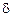, measured in 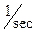, is called the damping factor. Calculate the velocity and acceleration of motion expressed by the formula

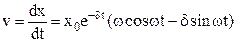, (8.45)

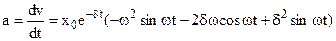(8.46)

Substituting x, v and a in (8.44 ), we obtain

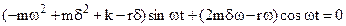(8.47)

This equation holds good at any instant (at any combination of sin 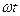and cos 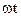), which is possible if the coefficients before sine and cosine equal zero. Then

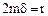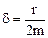; (8.48)

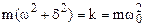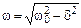; (8.49)

Date: 2015-01-12; view: 918