
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Addition of mutually perpendicular vibrations
To analyze a complex vibration consisting of the sum of two mutually perpendicular vibrations, it is best to use an electronic oscilloscope.
Let us assume that the vibration of the beam trace is the vertical direction is represented by relation
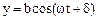 (8.54)
(8.54)
and in the horizontal direction by the relation
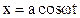 (8.55)
(8.55)
To determine the nature of the resultant path we must eliminate time from the above equations and obtain an equation of the form
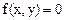 (8.56)
(8.56)
Writing the expressions for the displacements in the form
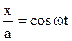 ,
, 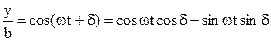 (8.57)
(8.57)
and replacing, in the second equation, 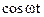 by
by 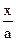
and  by
by  ,
,
we obtain after simple conversion the equation of an ellipse rotated with respect to the coordinates axes:
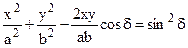 (8.58)
(8.58)
Let us now vary the parameters of the vibrations and see what happens to the ellips. If we vary the phase difference, the ellipse will change its form and simultaneously rotate.
Let us return to the original equations. Let us assume that the frequency of the vertical vibration 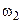 is
is 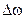 greater than the frequency of the horizantal vibration
greater than the frequency of the horizantal vibration 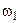 . Then
. Then
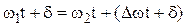 , (8.59)
, (8.59)
where the variable phase difference is within the brackets. If the frequencies differ considerably from each other, before the beam is able to describe the major portion of one ellipse the phase has already changed. As a result, the described curves look less and less like ellipse. Examples of these queer curves are known as Lissajous Figures.
In the intermediate case, the amplitude assumes a value between zero and 2A. Another important case is the additional of vibrations having different frequencies. For simplicity let us assume that 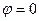 and the amplitudes are equal. Them
and the amplitudes are equal. Them
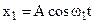 ,
, 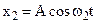 (8.60)
(8.60)
and
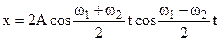 (8.61)
(8.61)
In the general case, the vibration motion obtained when such vibrations are added does not exhibit a distinct periodicity with respect to the displacement x.
Date: 2015-01-12; view: 1744
| <== previous page | | | next page ==> |
| Forced vibrations | | | Additional of parallel vibrations |