Rotation of Rigid Body

“Perfectly rigid” bodies means that we may neglect any deformation occurring during the motion of such a body, and assume that the distances between the particles of the body remain unchanged.

Let us consider a rigid body rotating about a fixed axis passing through it. We are interested in the kinetic energy of rotation of the entire rigid body, which is composed of the kinetic energies of the individual particles

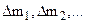
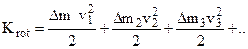(6.6)

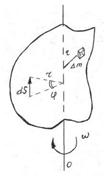
Figure 6.2

Angular velocity is

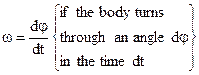(6.7)

But ,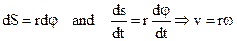

where v is linear velocity. Thus, the formula K_rot may be written in the following form

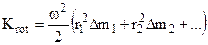(6.8)

The quantity in brackets does not depend on the velocity of motion, but is a measure of the inertial properties of a body executing rotational motion.

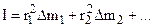is called the moment of inertia of the body.

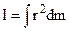(6.9)

The formula for a body’s kinetic energy of rotation acquires form

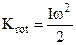(6.10)

If we carefully examine the formula for moment of inertia, we see that the value of I depends on the nature of the distribution if the mass with respect to the axis of rotation.

Let us calculate the moment of inertia of a flat disk, of radius r, relative to the axis perpendicular to the plane of the disk and passing through its center. The mass of an annular element of radius x is

, (6.11)

where 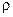is the density of the disk’s material. This ring has a moment of inertia

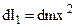(6.12)

and the moment of inertia of the entire disk is

(6.13)

The moment of inertia depends on the orientation of the axis and the location of the point through which is passes. If the axis of rotation is displaced relative to the center of mass by the amount a, I, the new moment of inertia, will differ from I₀, the moment of inertia with respect to the parallel axis passing through the center of mass.

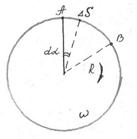
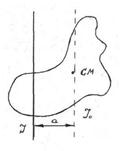
Figure 6.3. We can express the kinetic energy of a body rotating about the displaced axis at the sum

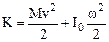(6.14)

where v is the velocity of motion of the center of mass and is equal to aω. Thus,

(6.15)

Hence, the moment of inertia I with respect to a parallel axis, displaced by a distance a from the center of mass, can be expressed as follows

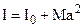. (6.16)

Moment of inertia in common case may be calculated from the relation

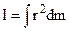. (6.17)

Date: 2015-01-12; view: 887