Mass and Energy

One of the great conservation laws of science has been the law of conservation of matter. The Roman poet Lucretus wrote: “Things cannot be born from nothing, cannot when begotten be brought back to nothing”.

Albert Einstein suggested that, if certain physical laws were to be retained, the mass of a particle had to be redefined as

m= 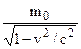or m =m₀ (1- 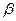²)^-1/2 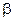=v/c (5.36)

Here m₀ is the mass of the particle which is at rest with respect to the observer, called the rest mass of the particle measured as it moves at a speed v relative to the observer, and c is the speed of light, heaving a constant value of approximately 300·10³ kmeters/sec.

To find the kinetic energy of a body, we compute the work done by the resultant force in setting the body in motion. We obtained

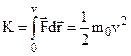(5.37)

for kinetic energy, when we assumed a constant mass m₀.

Suppose now instead we take into account the variation of mass with speed and use

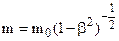(5.38)

in our previous equation. We find that the kinematics energy is no longer given by 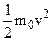but instead is

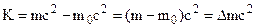. (5.39)

The basic idea that energy is equivalent to mass can be extended to include energies other than kinetic. When we compress a spring and give it elastic potential energy U, its mass increases from m₀ to

(5.40)

When we add heat in amount Q to an object, its mass increases by an amount 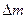, where

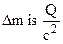. (5.41)

We arrive at a principle of equivalence of mass and energy. For every unit of energy E of any kind supplied to a material object increases by an amount

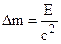(5.42)

This is the famous Einstein formula

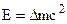. (5.43)

Date: 2015-01-12; view: 845