Fundamental equation of motion for a rotating body

The force 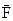is applied at a point located at a distance r from the axis of rotation. The angle between the direction of the force and the radius vector is designated by 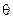. Since the body is perfectly rigid, the work of this force is equal to the work expended in rotating the entire body. In rotating the body through an angle , the point of application traverses the path 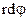and the work dA, equal to the product of the projected force along the direction of displacement and the magnitude of the displacement, is then

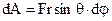(6.18)

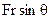is the moment of force or torque.

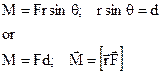
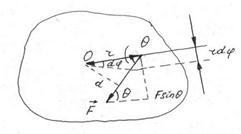
Figure 6.5

The torque is equal to the product of the force and the lever arm. The formula for work that we have sought is

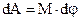(6.19)

The work of rotating a body is equal to the product of effective torque and the angle of rotation. The work of rotation goes to increase the kinetic energy of rotation. Hence, the following equation must hold

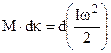(6.20)

If the moment of inertia is constant for the time of motion, then

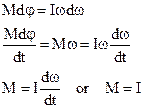(6.21)

This is the fundamental equation of motion for a rotating body. The torque on a body is equal to the product of the moment of inertia and the angular acceleration. The quantity analogous to 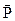is the moment of momentum or angular momentum.

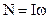(6.22)

It can be rigorously proved that angular momentum satisfies the law of conservation in a closed system – the total angular momentum of the bodies belonging to this system does not change.

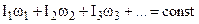(6.23)

Date: 2015-01-12; view: 1076