
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Kinetic Energy and the Work-Energy Theorem
Let us suppose now that the resultant force acting on an object is zero, so that the object is accelerated. Let us choose that x-axis to be in the common direction of 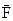 . What is the work done by this force on the particle in causing a displacement x? We have
. What is the work done by this force on the particle in causing a displacement x? We have
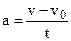 and
and 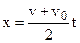 (5.10)
(5.10)
If t=0, then v=v0. Then the work done is
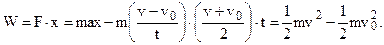 (5.11)
(5.11)
We call one-half the product of the mass of a body and the square of its speed the kinetic energy of the body.
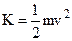 (5.12)
(5.12)
The work done by the resultant force acting on a particle is equal to the change in the kinetic energy of the particle.
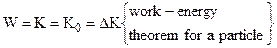 (5.13)
(5.13)
Kinetic energy is a function of the state of motion. If the kinetic energy changes from K1 to K2, then the work performed there by is equal to K2 - K1, independent from the nature of the motion.
Let us consider several phenomena in witch the performed work is not accompanied by a change in the velocity of the body. We shall concern with two deformations of a body, while the second deals with events occurring during the motion of a body in a gravitational or electric field.
The function of state or the function of the body’s properties and degree of deformation is called the potential energy of elasticity. The work expended in stretching the body from length 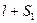 to length
to length  where l is the length of the outstretched spring, is
where l is the length of the outstretched spring, is
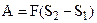 (5.14)
(5.14)
Hook’s law:
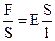 (5.15)
(5.15)
where E is the modulus of elasticity and S is the cross-section of the stretched body. Thus, the stiffness has the value
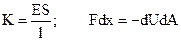 (5.16)
(5.16)
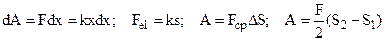 (5.17)
(5.17)
In the expression for work, we must use the average value of the force F. We then obtain
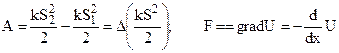 (5.18)
(5.18)
The work against the elastic force is expended in increasing the quantity 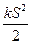 . The quantity
. The quantity
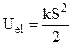 (5.19)
(5.19)
will be called elastic potential energy.
Gravitational force possesses the same feature as elastic force. The body is located close to the Earth’s surface. From point L, the body is moved to the higher point 2 along some curvilinear path. Let us divide this path into small segments, replacing the curved line by a broken line. The work expended in moving a body along one of these linear segments of length dl then
 (5.20)
(5.20)
where dh is the increase in height. For work expended along the entire path
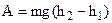 (5.21)
(5.21)
where h1 and h2 are the height of points 1 and 2 respectively. Furthermore
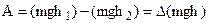 (5.22)
(5.22)
It is quite evident that
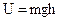 (5.23)
(5.23)
gravitational potential energy.
Let us assume that two attracting bodies draw together along the line of action of the forces over an infinitely small segment – dr of the path.
Thus
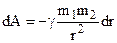 (5.24)
(5.24)
But 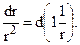 Therefore
Therefore
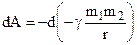 . (5.25)
. (5.25)
Work takes place at the expense of a decrease in the value of 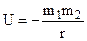 , which is a measure of the gravitational energy in the general case.
, which is a measure of the gravitational energy in the general case.
 (5.26)
(5.26)
The ratio of the amount of work A done in moving any particle of mass m from a given point to infinity and the mass of this particle is called the potential of the gravitational field in the given point. At the distance r from the center of the Earth the potential of the gravitational field  equals
equals
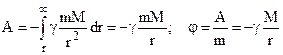 . (5.27)
. (5.27)
The work and the potential are negative since the force of gravity becomes an obstacle to this displacement. The work done in moving the particle from one point in the gravitational field “1” to another “2” equals
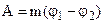 (5.28)
(5.28)
The gravitational field is potential. The law of universal gravitation served as a basis for computing the masses of the Earth, Sun, Moon and planets. The mass of the Earth is 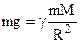 .
.
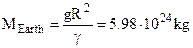
The mass of the Sun MSun may be determined from the period of rotation T of planets. Along the orbit of each planet the force of attraction is centripetal, therefore
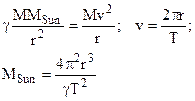 (5.29)
(5.29)
And thus, for two planets we obtain
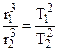 (5.30)
(5.30)
in other words, the squares of the times taken to describe their orbits by two planets are proportional to the cubes of the major semiaxes of the orbits (Kepler’s Law).
Irrespective of the type of forces involved in the motion; the work of the resultant force is always equal to the increment of the body’s kinetic energy
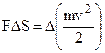 (5.31)
(5.31)
or in another form
 (5.32)
(5.32)
Here Fpot is potential forces; f is non potential forces. The work for f forces is equal to the change in the internal energy of a body or the medium in which the body moves. Substituting in place of the work of the potential forces the increment of potential energy with reversed sing, we can write
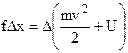 (5.33)
(5.33)
The sum of a body’s potential and kinetic energy is called total mechanical energy.
 (5.34)
(5.34)
The change in a body’s total energy is equal to the work of no potential forces. For a system consisting of many bodies the total energy will be equal
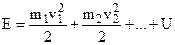 (5.35)
(5.35)
If all the interacting bodies are taken into account (close system), from of the law remains the same as for a single body. If the work of the no potential forces is negligible, the total mechanical energy of a closed system of bodies remains unchanged or is conserved. It is the law of conservation of mechanical energy.
According to the International System of Units the work and energy are measured in Joules. Joule is the amount of work done in applying one Newton through one meter of a distance traversed by the point of application of this force in the direction of the force:
Joule = Newton x meter.
According to CGS system – ergs:
Date: 2015-01-12; view: 1172
| <== previous page | | | next page ==> |
| Mechanical Energy | | | Mass and Energy |