Mechanical Energy

Let a body be acted upon by a number of forces whose vector sum is equal to zero. The body moves uniformly and rectilinearly. All the forces may than be resolved into four components.

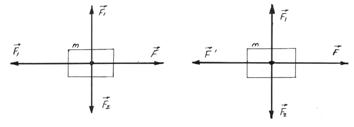
Figure 5.1

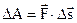(5.4)

Forces 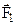and 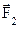in accordance with the adopted definition, perform no work. Force 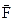performs work equal to 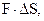where 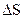is the traversed distance. The work of force 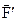is equal to 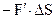, where the minus sing indicates that work is performed against the force .

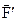Let us now consider the motion of a body with acceleration (curvilinear and non uniform motion). Now, 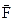is not equal to 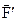, and 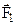is not equal to 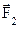. The work of force 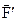is again negative, i.e., the work is performed against the force 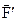and equal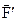

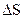
The inequality between the forces 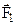and 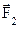shows that the motion is curvilinear. Their difference 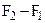corresponds to the normal component of the acceleration. Let us consider an extreme case – uniform motion in a circle. The resultant force for such motion is directed, as we know, along the radius of the circle, i.e., perpendicular to the direction of motion. Therefore, the centripetal force performs no work. 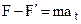is the tangential component of the resultant force 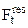, and

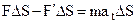(5.5)

The work expended in accelerating a body is equal to the product of the mass of the body, the traversed distance, and the tangential acceleration. The work performed by the force of resistance and the work expended in accelerating the body

(5.6)

For 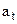, we obtain

; (5.7)

where v is the average velocity, which is equal

(5.8)

Since 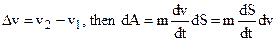or 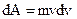. In result 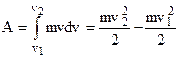. (5.9)

Date: 2015-01-12; view: 1386