Projectile Motion

An example of curved motion with the constant acceleration is the projectile motion. This is the two-dimensional motion of a particle thrown obliquely into the air. If we choose a reference frame with the positive y-axis vertically upward, we may put

. (3.8)

Let us further choose the origin of our reference frame to be the point at which the projectile begins its flight

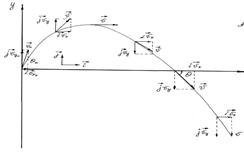
Figure 3.2

The velocity at t = 0, the instant the projectile begins its flight, is 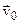, which makes an angle 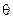₀ with the positive x-direction. The x – and y-components of 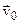are then

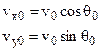. (3.9)

The horizontal velocity component retains its initial value throughout the flight, so that

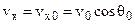. (3.10)

The vertical component of the velocity will change with the same in accordance with vertical motion with the constant downward acceleration

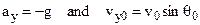(3.11)

so that

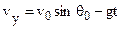. (3.12)

The magnitude of the resultant velocity vector at any instant is

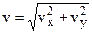. (3.13)

The angle 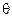that the velocity vector makes with the horizon at that instant is given by

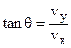(3.14)

The x-coordinate of the particle’s position at any time is

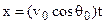. (3.15)

The y-coordinate is

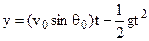(3.16)

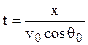(3.17)

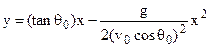(3.18)

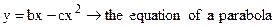(3.19)

Let us suppose that we know the change of acceleration with time, i.e., the function

, (3.20)

then the velocity of the particle at the instant t may be easily found

. (3.21)

The less 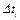is the more accurate will be the calculation, that is why the value of 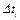must be taken infinitesimal. In this case the sum 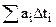is written as an integral

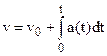. (3.22)

If the body moves with variable acceleration the path covered by it is defined in the same way.

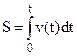. (3.23)

Fig. 3.3 gives a graphical explanation of this calculation. This path is represented by the area

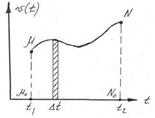
Figure 3.3

Date: 2015-01-12; view: 1052