
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Circular Motion of a Particle
A motion, in which all points of a body describe circumferences about a certain axis, is called a rotational motion. We meet some new quantities studying kinematics of rotation. At first let us innumerate them: Dφ - angle of rotation; 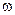 - angular velocity;
- angular velocity; 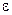 - angular acceleration; T – period of rotation; ν - frequency of rotation.
- angular acceleration; T – period of rotation; ν - frequency of rotation.
Let us suppose that a particle performs its motion in circle with radius R and at the initial t0 it is located at point A. The displacement of a particle can be expressed by the formula 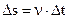 , but
, but
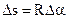 ,
, 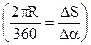 (3.24)
(3.24)
and we obtain
 . (3.25)
. (3.25)
Where 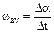 is the ratio between the angle of rotation of the radius-vector and the corresponding time interval? This relation is termed the average angular velocity of rotation. When
is the ratio between the angle of rotation of the radius-vector and the corresponding time interval? This relation is termed the average angular velocity of rotation. When 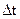 tends to zero we have:
tends to zero we have:
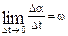 , (3.26)
, (3.26)
i.e. obtain the angular velocity of rotation at the time instant t.
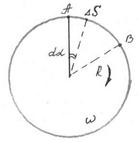
Figure 3.4
For the average angular acceleration
 , (3.27)
, (3.27)
and instantaneous acceleration
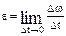 . (3.28)
. (3.28)
We may obtain
 . (3.29)
. (3.29)
For uniformly accelerated rotary motion we obtain
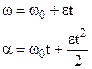 . (3.30)
. (3.30)
The normal acceleration of a particle moving along a circle with the radius R can be expressed as a function of the angular velocity of rotation
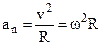 . (3.31)
. (3.31)
The angular velocity of rotation is a vector 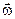 directed along the axis rotation. The direction
directed along the axis rotation. The direction 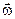 is defined by applying the so–called right-hand rule, i.e. in the direction of translational motion of the screw having the same rotation.
is defined by applying the so–called right-hand rule, i.e. in the direction of translational motion of the screw having the same rotation.
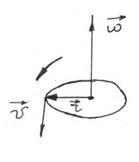
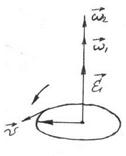
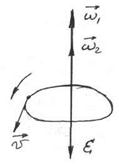
Figure 3.5
The angular acceleration 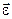
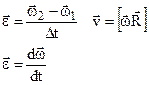 . (3.32)
. (3.32)
The period of rotation T is the time of one complete revolution. In this case Dj= 2π
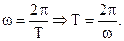 (3.33)
(3.33)
Principles of relativity by Galileo
Let us consider two references systems, moving relatively to each other with constant velocity. Lets find the relationship between x, y, z and x1, y1, z1 of point P. If the count of time is started from the moment, when origin of coordinates of both reference systems is coincided, then
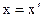 . (3.34)
. (3.34)
Transformation of Galiley
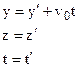 . (3.35)
. (3.35)
(time in both system flows equally) Applicable if
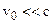 . (3.36)
. (3.36)
Lets find the relationship between velocities
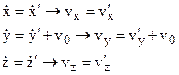 (3.37)
(3.37)
Or in vector form
 . (3.38)
. (3.38)
The rule of adding velocities under free choice of the mutual directions of the coordinate axes 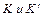 . Any reference system moving relatively to some inert system with constant velocity will also be inert. Equation of motion does not change when transferring between inert references systems
. Any reference system moving relatively to some inert system with constant velocity will also be inert. Equation of motion does not change when transferring between inert references systems
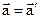 . (3.39)
. (3.39)
Lecture 4. Particle dynamics
In this lecture and the next we discuss the causes of motion, an aspect of mechanics called dynamics. The motion of a given particle is determined by the nature and the arrangement of the other bodies that form its environment.
Dynamics deals with the motion of bodies under the effect of forces. The basic concepts of dynamics are mass, impulse and force.
The mass is a property of any body. The body property to resist of the acceleration under the effect of force is called mass [m]=[kg].
Density is the mass per unit of volume:
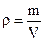 . (4.1)
. (4.1)
Impulse (linear momentum) is the product of mass by velocity. It is a vector quantity
 (4.2)
(4.2)
Force – the physical quantity resulting on the interaction of bodies. The unit of force is a Newton: [F]=N.
In what follows, we limit ourselves to the very important special case of gross object moving at speeds that are small compared to c, the speed light; this is the realm of classical mechanics:  << c, c = 108 m/s.
<< c, c = 108 m/s.
The central problem of classical particle mechanics is this:
- we are given a particle whose characteristics we know;
- we place this particle, with a known initial velocity, in an environment of which we have a complete description: v0, g =9,8 m/c2, x0 , y0.
Problem: what is the subsequent motion of the particle? x = f(t); y = f(t).
This problem was solved by Isaac Newton (1642-1727) when he put forward his laws of motion and formulated his law of universal gravitation.
We introduce the concept of force and define it in terms of the acceleration and experienced by a particular standard body:
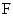 ~
~  (4.3)
(4.3)
We develop a procedure for assigning a mass m to a body so that we may understand the fact that different particles of the some kind experience different acceleration in the same environment. Finally, we try to find the ways of calculating the forces that act on particles from the properties of the particle and its environment; that is, we look for force laws.
Galileo asserted that some external force was necessary to change the velocity of a body but that no external force was necessary to maintain the velocity of a body. For example, exerts a force on the block when it sets in motion. The rough plane exerts a force on it when it slows it down. Both of these forces produce a change in the velocity, that is, they produce acceleration.
This principle of Galileo was adopted by Newton as the first law of motion: “Every body persists in its state of rest or of uniform motion in a straight line unless it is compelled to change that state by forces impressed on it.”
The first law tells us that, if there are no nearby object then it is possible to find a family of reference frames in which a particle has no acceleration. Newton’s first law is often called the law of inertia and the reference frames to which it applies are therefore called inertial frames. When several forces act on a body, each produces its own acceleration independently. The resulting acceleration is the vector sum of the several independent accelerations.
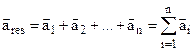 (4.4)
(4.4)
What effect will the same force have on different object? The same force will produce different accelerations on different bodies. We define the ratio of the masses of the two bodies to be the inverse ratio of the accelerations given to these bodies by the same force, or
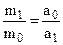 (same force
(same force 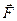 acting) (4.5)
acting) (4.5)
We can now summaries all the experiments and definitions described above in one equation, the fundamental equation of classical mechanics:
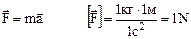 (4.6)
(4.6)
Newton’s second law:
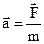 (4.7)
(4.7)
The acceleration of the body is directly proportional to the resultant force acting on it and parallel in direction to this force and that the acceleration, for a given force, is inversely proportional to the mass of the body.
Classification of forces
We consider three kinds of the forces in dynamics:
1) Gravity force - according to the law of universal gravitation the force between two point masses 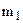 and
and 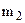 is equal to:
is equal to:
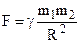 . (4.8)
. (4.8)
Weight of gravity: 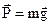 , (4.9)
, (4.9)
g - is the acceleration in a force form.
2) Force of friction. When two contacting solid bodies are in motion relative to each other force arises which hinders their motion. This force is called the force of friction.
However, the forces of friction can exist when bodies are at rest. The force of friction is caused by the irregularities of the contacting surfaces. The friction force is given by:
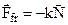 . (4.10)
. (4.10)
The friction is observed in liquids and gases too, in this case
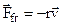 , (4.11)
, (4.11)
where r is the coefficient of the medium resistance. One may see that friction force is directly proportional to the velocity.
3) When a body is subjected to decoration, the elastic force arises. The magnitude of elastic force is directly proportional to the strain. According to the Hook’s Law
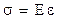 , (4.12)
, (4.12)
where s (sigma) – is the stress, 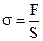 ;
; 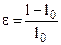 - strain; E - Young’s modulus. The last value is a material constant. Units of this values: [s]=
- strain; E - Young’s modulus. The last value is a material constant. Units of this values: [s]= 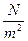 =[Pa].
=[Pa].
Date: 2015-01-12; view: 1397
| <== previous page | | | next page ==> |
| Projectile Motion | | | Frictional forces |