Lecture 3. Constant Acceleration

Let 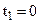and let 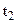be any arbitrary time t. Let 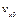be the value of 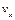at t=0 and let 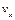be its value at the arbitrary time t. With this notation we find from

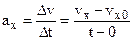(3.1)

or

.

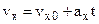The equation states that the velocity 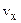at time t is the sum of its value 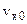at time t=0 plus the change in velocity during time t, which is .

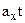When the velocity 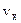changes uniformly with time, its average value over any time interval equals one-half the sum of the values of 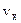at the beginning and the end of the interval.

That is the average velocity 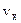between t₁ = 0 and t₂ = t is

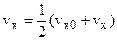. (3.2)

If the position of a particle at t=0 is x₀ , the position x at time t can be found from

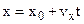. (3.3)

If then

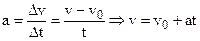. (3.4)

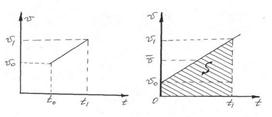
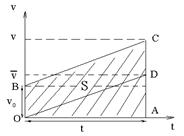
Figure 3.1

For the path we have 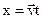and (fig. 3.1), then

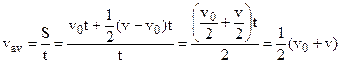
or 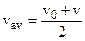. (3.5)

In result we have

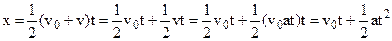. (3.6)

Galileo’s Experiment

Galileo Galilei (1564-1642), an Italian scientist of the Renaissance has showed that the character of the motion of a ball rolling downwards on inclined surface was the same as that of a ball in free fall. The inclined surface merely served to reduce the effective acceleration of gravity and to slow the motion thereby. Time intervals measured by the volume of water discharged from a tank could then be used to test the speed and acceleration of this motion. Galileo showed that if the acceleration along the incline is constant, the acceleration along the incline is simply a component of the vertical acceleration of gravity, and along an incline if constant slope the ratio of two acceleration remains fixed.

He found from his experiments that the disproportion covered in consecutive time intervals were proportional to the odd numbers 1, 3, 5, 7…etc. Total distances for consecutive intervals thus were proportional to 1+3, 1+3+5, 1+3+5+7, etc., that is to the squares of the integers 1, 2, 3, 4, etc.

But if the distance covered is proportional to the square of the elapsed time, velocity acquired is proportional to the elapsed time, a result which is true only if motion is uniformly accelerated, He found that the same results were shown regardless of the mass of the ball used.

We shall select a reference frame rigidly attached to the earth. The y-axis will be taken as positive vertically upward. Then the acceleration due to gravity will be a vector pointing vertically down in the negative y-direction. (This choice is arbitrary). Then we have

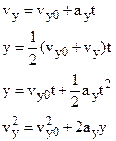, (3.7)

were .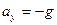

Date: 2015-01-12; view: 1051