Ultimate velocity

If body begins motion from condition of rest and moves with acceleration, its velocity in time t will be:

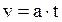. (2.13)

Consequently, for any different from zero value of acceleration "a" during long enough time "t" it is possible to obtain any great value of the velocity. However, this does not occur. According to the theory of relativity

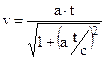. (2.14)

If 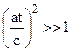, then

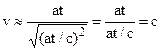. (2.15)

Velocity of the light in seconds is an ultimate physical velocity c = 3 ·10⁸ м/с.

Tangential and normal accelerations

It is customary to resolve the acceleration vector into two components

(2.16)

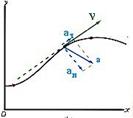
Figure 2.4

The vector 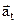, directed along the curve, represents the change in the magnitude of the velocity and is called the tangential acceleration.

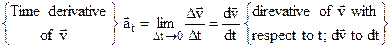.(2.17)

The vector 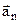, directed normal to the curve, represents the change in the direction of the velocity and is called the normal acceleration.

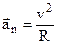, (2.18)

where R is the radius of curvature at the given point.

The normal acceleration 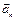is often also called the centripetal acceleration. There are following simple relations between the period T, the frequency ν and the angular velocity w:

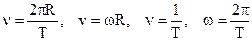(2.19)

The motion, being the function of tangential and normal components of acceleration, is classified as follows:

1) 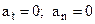- uniform and rectilinear motion;

2) 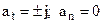- uniformly accelerated (+j) or uniformly retarded (-j) rectilinear motion;

3) 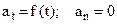- rectilinear variably accelerated motion;

4) 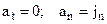- circular uniform motion, the radius of the circle is determined by the velocity of motion and the magnitude , as given in formula ;

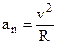5) 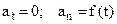- curvilinear uniform motion;

6) 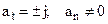- curvilinear uniformly accelerated (retarded) motion;

7) 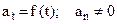- curvilinear variably accelerated motion.

Date: 2015-01-12; view: 1102