
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Binary Encoders
A 2n-input binary encoder is a combinational system that has 2n inputs x = ( 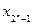 , . . . , x0) and n outputs y= (
, . . . , x0) and n outputs y= ( 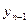 , . . . , y0), as shown in Figure 1.30. It performs the inverse function of a decoder: it is a code converter from the "l-out-of-2n"' code to a binary code. That is, only one of the input variables has value 1 at a time and the outputs represent, in a binary code, the index of the input with the value 1. When more than one input has the value 1, the output is undefined.
, . . . , y0), as shown in Figure 1.30. It performs the inverse function of a decoder: it is a code converter from the "l-out-of-2n"' code to a binary code. That is, only one of the input variables has value 1 at a time and the outputs represent, in a binary code, the index of the input with the value 1. When more than one input has the value 1, the output is undefined.
The module also has an enable input E and a module active output A. This output indicates that there is an input with a value 1 ("active"). The input E and the output A are used in designing networks of encoder modules.
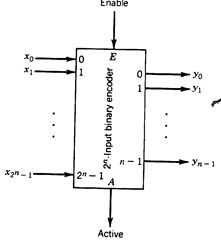
Fig. 1.30 - 2-input binary encoder.
A high-level description is
| y= | I if xi=1 and (xk=0, k¹i) and E=1 |
| 0 otherwise |
| A= | 1 if some xi=1 and E=1 |
| 0 otherwise |
where
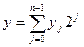
and
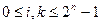
In the description of combinational systems, this module is denoted by
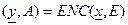
For example, ENC((0,0,0,1,0,0,0,0),1) = ((1,0,0),1).
The switching expressions that represent a binary encoder are
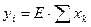
where xk is included in the sum if the ith bit of the binary representation of k is 1, and
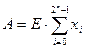
For example, the switching expressions representing an 8-input binary encoder are
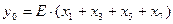
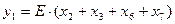
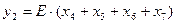
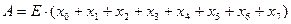
A gate-network implementation of an 8-input binary encoder is given in Figure 1.31. A binary encoder is used whenever the occurrence of one of several disjoint events is to be represented by an integer identifying the event.
To facilitate the design of larger encoders, the encoder module usually has the wired-OR capability. Encoders exist for other than binary codes (BCD, Gray, etc.).
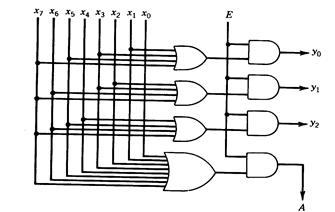
Fig. 1.31 - Implementation of an 8-input binary encoder.
Date: 2015-01-12; view: 1386
| <== previous page | | | next page ==> |
| Coder units | | | Priority Encoders |