Coder units

Encoder Networks

A network of 2k-input encoders and some other modules can implement a 2n-input encoder. We assume in the following discussion that n = 2k.

Consider first the case of encoder networks when at most one input x_i can have a value 1. The priority encoder networks will be discussed later.

We introduce these networks with an example. Consider a 64-input encoder network using eight-input encoders as shown in Figure 1.28. The network consists of two levels of modules. In the first level there are eight encoders, each of them encoding a part of the input vector x. Since there is only one input with value 1, the outputs of all encoder modules are 0 except the one corresponding to this x_i= 1. Also, only the corresponding A has value 1. Consequently, the outputs of the encoders are

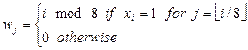
and

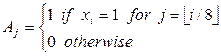
In the second level there are three OR gates with eight inputs each which produce (y₂, y₁, y₀), and an eight-input encoder to encode the A outputs of the first-level encoders and produce (y₅, y₄, y₃).

The connection of the OR gates produces

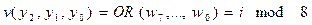
since all w's except one are 0.

Similarly the output of the second-level encoder is

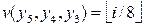
and, therefore, and the network performs the encoding function. The OR gates can be eliminated if a wired-OR technology is used as indicated in Figure 1.28.b. In this figure we indicate also the outputs when x₁₇=1.

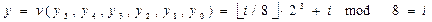
This scheme can be generalized as follows. For an 2ⁿ-input encoder, using 2^n/2-input encoder modules, the first level is formed of 2^n/2 encoder modules, which receive the corresponding input subvectors. The second level is formed of n/2 OR gates, which collect the corresponding outputs of the first-level encoders and produce the n/2 least significant bits of the output. For the n/2 most significant bits, another encoder module is used to encode the A outputs of the first-level encoder modules. The generalization for n=rk is left as an exercise.

We now consider the implementation of priority-encoder networks where the priority of the input x_i, is higher than the priority of x_j for i>j. A 2ⁿ-input priority encoder can be implemented by a network of 2^n/2-input priority encoders, OR gates, and a 2^n/2-input priority encoder as illustrated in Figure 1.29. The analysis of this network is left as a problem (Exercise 4.36). Note that the delay of the network is high since the enable signal has to propagate through all encoder modules of the first level.

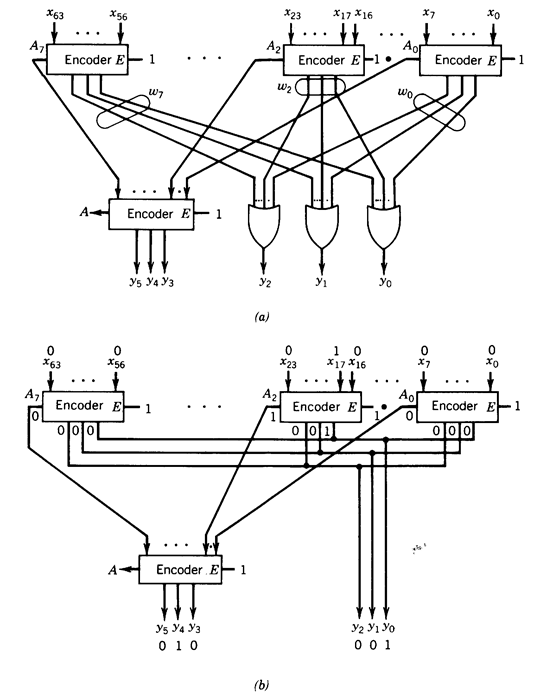
Fig1.28 - Encoder networks (a) OR gates and (b) with wired-Ors.

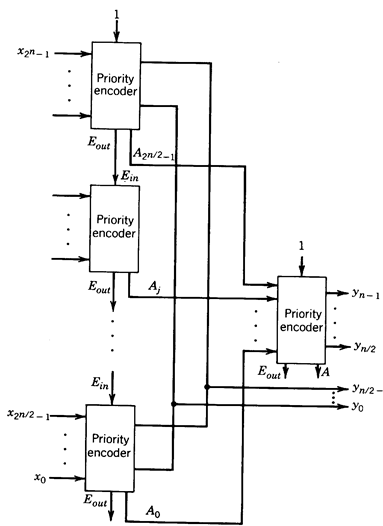
Fig. 1.29 - Priority encoder network.

Date: 2015-01-12; view: 1208