Brief theoretical information

The transient process of connecting a charged capacitor with a capacitance C to a series-connected circuit from a resistor witch resistance R and coil witch inductance L can be described by the following equation

L ∙ C ∙ 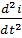+ R ∙ C ∙ 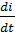+ i = 0,

where i ? the current in the circuit.

The characteristic equation for the last expression has the form:

L ∙ C ∙ p² + R ∙ C ∙ p + 1 = 0.

If the roots of this characteristic equation are complex conjugate:

?_1,2 = ̶ δ = ̶ δ ϳ ∙ ,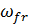

where δ = R / (2 ∙ L) is the attenuation coefficient;

? natural oscillation frequency;

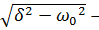frequency of free oscillations Փ,

that transition process will have an oscillatory damping character.

The solution of the equation describing the transition process is the following expression

i = ̶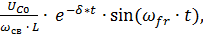

where U_C0 ? is the initial voltage on the capacitor.

The expression for the voltage on the capacitor with an oscillating damping nature of the transient process has the form

u_C = sin( ,

where U_C0 ? is the initial voltage on the capacitor;

ⱷ = arctg( 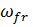/ δ).

The aperiodic transient process occurring at the capacitor discharge on a series connected RL-circuit is described by the same linear differential equation of the second order as the oscillating damping one. However, both roots of its characteristic equation will be valid negative:

p_1,2 = ̶ δ β,

where β =

The solution of the differential equation are can find as follows:

i = ̶ ̶ ).

The voltage on the capacitor with aperiodic nature of the transient process can find so:

u = ̶ ).

Procedure for conducting experiments

Experiment 1. Investigation of the transient process caused by capacitor discharge through a series-connected resistor and inductor with complex conjugate roots of the characteristic equation

Build the scheme, which is shown in fig. 6. 3.

Fig. 6. 3. The scheme for the study of the transition process caused by the discharge of the capacitor through a series-connected resistor and inductor, with complex conjugate roots of the characteristic equation

Enable the simulation of the transition process. Double-click LMB on the sign of the oscilloscope to get the enhanced image. Set the following settings of the oscilloscope: horizontally-0.5 ms / div., vertical 2 V / div. Sketch the transition curve and add the simulation results to the table. 6. 5.

Table 6. 5

Results of studies of the transient process at the discharge of the capacitor on a series-connected circuit from the resistor and the inductor with complex conjugate roots of the characteristic equation

Calculate the current values in the circuit at the discharge of the capacitor at the time specified in the table. 6. 5, and write them down in the appropriate row of this table. Compare the results of the experiment and calculation.

Experiment 2. Investigation of the transient process caused by capacitor discharge through a series-connected resistor and inductor at the real negative roots of the characteristic equation

Build the scheme, which is shown in fig. 6. 4.

Fig. 6. 4. The scheme for the study of the transition process caused by the discharge of the capacitor through a series-connected resistor and inductor at the real negative roots of the characteristic equation

Turn on the modeling process. Double-click LMB on the sign of the oscilloscope to get the enhanced image. Set the following settings of the oscilloscope: horizontally - 0.5 ms / div., on vertically - 5 V / div. Sketch the transition curve and add the simulation results to the table. 6. 6. When measuring current and voltage on the oscilloscope screen, use visors to improve accuracy.

Table 6. 6

Results of studies of the transient process at the discharge of the capacitor on a series-connected circuit from the resistor and the inductor at the real negative roots of the characteristic equation

Calculate the current values in the circuit at the discharge of the capacitor at the time specified in the table. 6. 6, and write them down in the appropriate row of this table. Compare the results of the experiment and calculation.

Literature

1. Danilov I. A. General electrical engineering: a textbook for colleges and technical schools / I. A. Danilov. ? M.: Higher. SHK., 2009. - 673 p.

2. Kasatkin A. S. Electrical engineering: textbook for universities / A. S. Kasatkin, M. V. Nemtsov. ? 12th ed., erased. - M.: publishing center "Academy", 2008. - 544 p.

3. Nemtsov M. V., Electrical engineering and electronics: textbook for universities / M. V. Nemtsov. ? M.: Moscow power engineering Institute "engineering and technology", 2003. - 616 p.

4. I. I. Ivanov Electrical engineering: a textbook for students elektrotekhnicheskikh specialties of universities / I. I. Ivanov, G. I. Soloviev, V. S. Radonic. - Krasnodar: LAN, 2005. - 496 p.

5. G. G. Rekus Collection of problems and exercises in electrical engineering and basics of electronics: textbook for universities / G. G. Rekus, and A. I. Belousov, M.: Higher. SHK., 2001. - 416 p.

6. Electrical engineering and electronics in experiments and exercises: Workshop on Electronics Workbench: in 2 vol. / D. I. Panfilov [et al.]; under the General ed. D. I. Panfilov. ? M.: DODEKA, 2000.

7. Zagidullin R. sh Multisim, LabVIEW and Signal Express. The practice of computer-aided design of electronic devices: reference edition. / R. Sh., Zagidullin. M.: Hot line ? Telecom, 2009. - 366 p.

8. Gavrilov L. P. Calculation and simulation of electrical circuits with the use of the PC: proc. manual for students mechanical engineer. universities / L. P. Gavrilov, D. A. Sosnin. ? M.: SOLON-Press, 2004. - 448 p.

9. Karlashchuk V. I. Electronic laboratory on IBM PC. Laboratory workshop on basis of Electronics Workbench and MATLAB. 5th ed. / V. I. Karlashchuk. ? M.: SOLON-Press, 2004. - 800 p.

APPLICATION

________________________________________________

Date: 2018-08-27; view: 28358