
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Tangential-Orbit Maneuver
Tangential-orbit maneuver occurs at the point where the velocity vector of spacecraft is tangent to its position vector, typically at perigee point.
| Example 9-1 | ||||||
| Determine the ∆V required to transfer from a circular orbit into elliptic orbit. | ||||||
| Solution | ||||||
The ∆V between two orbit can be shown as follow:

Figure 9-6 shows a typical tangential orbit maneuver at perigee point. Using the equation 9-5, the ∆V required is,
|
Non-Tangential Coplanar Maneuver
The orbit maneuver does not limited only at apogee and perigee point. If condition is allowed, the satellite able to perform the orbit maneuvers at any point.
Figure 9- 1 shows the ∆V vector required for a non-tangential orbit maneuver, where α is the difference angle between the flight path angle of V1 and V2.


| ( 9‑6 ) |
Hohmann Transfer
The Hohmannís transfer is the minimum two-impulse transfer between coplanar circular orbits. It can be used to transfer a satellite between two nonintersecting orbits (Walters Hohmann 1925).
The fundamental of the Hohmannís transfer is a simple maneuver. This maneuver employs an intermediate elliptic orbit which is tangent to both initial and final orbits at their apsides. To accomplish the transfer, two burns are needed. The first burn will insert the spacecraft into the transfer orbit, where it will coast from periapsis to apoapsis. At apoapsis, the second burn is applied to insert spacecraft into final orbit.
Figure 9-7 represents a Hohmannís transfer from a circular orbit into another circular orbit. A tangential ΔV1 is applied to the circular orbit velocity. The magnitude of ΔV1 is determined by the requirement that the apogee radius of the resulting transfer ellipse must equal the radius of the final circular orbit. When the satellite reaches apogee of the transfer orbit, another ΔV must be added or the satellite will remain in the transfer ellipse. This ΔV is the difference between the apogee velocity in the transfer orbit and the circular orbit velocity in the final orbit. After ΔV2 has been applied, the satellite is in the final orbit, and the transfer has been completed.

| (9‑7) |
| |

| (9‑8) | |||

| (9‑9) | |||

| (9‑10) | |||
| Example 9-2 |
| Determine the total ∆V required for Hohmann transfer to transfer from a LEO with hinitial = 191.344 km into GEO. |
| Solution |
The initial and final radius is,
rinitial = 191.344 + 6378.145 = 6569.489 km
rfinal = 42164.215 km
At first impulse, the delta-v required is,
 where,
where,
 Thus,
Thus,  For the second impulse, the delta-v required is,
For the second impulse, the delta-v required is,
 The total delta-v require is,
The total delta-v require is,
 km/sec km/sec
|
| Example 9‑3 |
Two geocentric elliptical orbits have common apse lines and their perigees are on the same side of the Earth. The first orbit has a perigee radius of  km and km and  , whereas for the second orbit , whereas for the second orbit  km and km and  . .
|
| Solution |
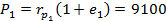 km km
 km km
 km/sec
For 2nd orbit: km/sec
For 2nd orbit:
 km & km &  km km
   km km
 km/sec
For transient orbit: km/sec
For transient orbit:
 km & km &  km km
 km km
 km/sec km/sec
 km/sec km/sec
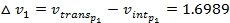 km/sec km/sec
 km/sec km/sec
 km/sec km/sec
 sec
Time of flight, TOF: sec
Time of flight, TOF:
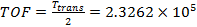 sec sec  hr hr
 km km
 km/sec
For 2nd orbit: km/sec
For 2nd orbit:
 km/sec
For transient orbit: km/sec
For transient orbit:
 km & km &  km km
 km km
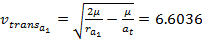 km/sec km/sec
 km/sec km/sec
 km/sec km/sec
 km/sec km/sec
 km/sec km/sec
 sec
Time of flight, TOF: sec
Time of flight, TOF:
 hr hr
|
| |
| A spacecraft is in a 300 km circular earth orbit. Calculate the transfer orbit time for a Hohmann transfer to a 3000 km coplanar circular Earth orbit. | |
| Solution | |
For initial orbit, 1:
 km km   km/sec
For final orbit, 3: km/sec
For final orbit, 3:
 km km   km/sec
For elliptical transient orbit, 2: km/sec
For elliptical transient orbit, 2:
 km km
 km km
 km
Transfer orbit time km
Transfer orbit time 
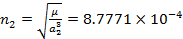 
 hr hr
|
Date: 2016-04-22; view: 1156
| <== previous page | | | next page ==> |
| Basic Orbital Maneuvers | | | Bi-elliptic Transfer |

 Figure 9-6. Single coplanar maneuver.
Figure 9-6. Single coplanar maneuver.

