Basic Orbital Maneuvers

Orbital Maneuvers

Sir Isaac Newton (1643-1727). English Physicist, Astronomer and Mathematician who described universal gravitation and the three laws of motion, laying the groundwork for classical mechanics, which dominated the scientific view of the physical Universe for the next three centuries and is the basis for modern engineering.

Philosophy is such an impertinently litigious lady that a man had as good be engaged in lawsuits as to have to do with her.

Isaac Newton in a letter to his friend Edmund Halley, June 20, 1687

9.

10.

Introduction

Orbital Energy

Spacecraft is not inserted in an orbit to stay forever! A spacecraft may need to change its orbit once or more during its life time due to many reasons. A launch vehicle may insert a geostationary (GEO) satellite into an initial low Earth orbit (LEO) which is much lower than the final operational orbit. Then, the satellite should transfer from the initial orbit to its final orbit. Another need may arise if a surveillance satellite has to change its orbit in order to track a new target. Interplanetary missions usually require many orbit transfers until the spacecraft is inserted into the operational orbit or to use the same spacecraft to accomplish more than one mission. At the satellite end of life (EOF), the satellite may be kicked out of its orbit whether to reenter the Earth’s atmosphere or to rest in a graveyard orbit.

Any analysis of orbital maneuvers, i.e., the transfer of a satellite from one orbit to another by means of a change in velocity, logically begins with the energy as

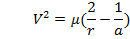
( 9‑1)

Where V is the magnitude of the orbital velocity at some point, r the magnitude of the radius from the focus to that point, a the semimajor axis

of the orbit, and μ the gravitational constant of the attracting body. Fig. illustrates r, V, and a.

Equation can be rearranged as

( 9‑2 )

Where it is evident that

Note that total energy/satellite mass is dependent only on a. asa increases, energy increases.

Figure 9- 1. Basic orbital maneuver.

Figure 9-2.Conservation of energy relates r, V and a.

Basic Orbital Maneuvers

Orbital maneuvers are based on the principle that an orbit is uniquely determined by the position and vector at any point. Conversely, changing the velocity vector at any point instantly transforms the trajectory to a new one corresponding to the new velocity vector. Any conic orbit can be transformed into another conic orbit by changing the spacecraft velocity vector.

9.2.1 Delta–V Budget

Orbital transfers are usually achieved using the propulsion system onboard the spacecraft. Since the propellant mass on board is limited, it is very crucial for mission planning to estimate the propellant required for every transfer. The overall need for propulsion is usually expressed in terms of spacecraft total velocity change, or DV (Delta-V) budget. We assume the propulsion is applied impulsively, i.e. the velocity change will be acquired instantaneously. This assumption is reasonably valid for high-thrust propulsion.

Figure 9-3. Delta-V Budget.

Figure 9-4. Impulsive thrust produced based on rocket theory.

From rocket theory shown in Figure 9-4, we can express the force produce by the impulsive thrust as:

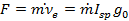
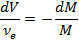
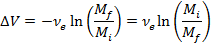
( 9‑3 )

where 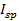=specific impulse = thrust/rate of fuel consumption. The spacecraft ‘sinitial and final mass, and the propellant mass are:

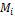= spacecraft initial mass

= spacecraft final mass

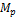=propellant mass used

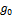=9.81m/s²

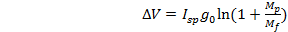
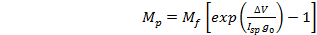
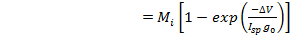
( 9‑4)

Satellite Launch

Figure 9-5. Satellite launch.

High-altitudes (above 200 km) may be achieved through two burns separated by coasting phase. The first burn is nearly vertical and places the satellite into an elliptic orbit with apogee at the final orbit radius. The satellite then coast (no burn) until it reaches the apogee. A second burn can be used to insert the satellite into its final LEO orbit.

Coplanar Maneuvers

When a satellite is launched, it can be placed into desired orbit through:

1. Directly from launch,

2. A booster at particular point to transfer into another orbit.

In section 9.3, the method (2) has been introduced, which is known as orbit maneuver. Orbit maneuver had its roots in the classical formulas and dynamics of Astrodynamics from several centuries ago. However, the application of orbit maneuver did not occur until after the launch of Sputnik in 1957.

Orbit maneuver is based on the fundamental principle that an orbit is uniquely determined by the position and velocity at any point. Therefore, changing the velocity vector at any point instantly transforms the trajectory to correspond to the new velocity vector. Thus, the orbit of a satellite is changed.

Coplanar maneuver only involves the change of semimajor axis and eccentricity of the orbit without changing the orbit plane. In this section, four kind of coplanar maneuvers are introduced:

i. Tangential-Orbit Maneuver,

ii. Non-tangential Orbit Maneuver,

iii. Hohmann Transfer,

iv. Bielliptic Orbit Transfer.

Date: 2016-04-22; view: 882