CATEGORIES:

Biology Chemistry Construction Culture Ecology Economy Electronics Finance Geography History Informatics Law Mathematics Mechanics Medicine Other Pedagogy Philosophy Physics Policy Psychology Sociology Sport Tourism

Bi-elliptic Transfer

Another type of orbit transfer that based on Hohmann transfer, which is called Bi-elliptic Transfer involves series of two Hohmann transfer.

Figure 9-8. Bielliptic Transfer.

The bi-elliptic transfer requires total of three impulse burn with two transfer orbit. The first burn is injected to insert the spacecraft into first transfer orbit at periapsis. When the spacecraft coasts to the apoapsis of the first transfer orbit, second impulse is injected to insert the spacecraft into second transfer orbit. Then, the spacecraft orbits along the transfer orbit to new apoapsis point. Finally, another impulse is injected to insert the spacecraft into the destination orbit. Figure 9-8 illustrates a bi-elliptic transfer between two circular orbits.

The bi-elliptic transfer requires much longer transfer time compared to the Hohmann Transfer. However, bi-elliptic is more efficient for long distance orbit transfer. Fig. 9-10 shows the cost comparison between Hohmann and Bi-elliptic Transfer. R is the ratio of final to initial radius for both orbits, where R* is the ratio of apogee radius of transfer orbit to initial orbit in bi-elliptic orbit. For R < 11.94, Hohmann transfer requires less cost than bi-elliptic transfer. For R > 15.58, bi-elliptic transfer performs better.

Figure 9-9.Delta-v Cost Comparison between Hohmann and Bi-elliptic Transfer.

Example 9-5

Determine the total ∆V required and time of flight for a bi-elliptic transfer with given orbit properties: Initial orbit, h_initial = 191.344 km Apogee altitude of transfer orbit, h_apog = 503873 km Final orbit, h_final = 376310 km

Solution

The initial, transfer orbit apogee and final radius are, r_initial= 191.344 + 6378.145 = 6569.489 km r_trans= 503873 + 6378.145 = 510251.145 km r_final= 376310 + 6378.145 = 382688.145 km And the semimajor axis for both transfer orbits are,

At first impulse, the delta-v required is,

At the second impulse, the delta-v required is,

At the third impulse, the delta-v required is,

The total delta-v require is,

The time of flight is,

Example 9-6

A spacecraft is in a 300 km circular Earth orbit. Calculate a. The total delta-v required for the bi-elliptical transfer to a 3000 km altitude coplanar circular orbit shown, and b. Compare the total transfer time with the Hohmann’s transfer time in Example 9-4.

Solution

a. For initial orbit, 1:

km/sec For final orbit, 4:

km/sec For first elliptical transient orbit, 2:

0.3

km/sec

km/sec For second elliptical transient orbit, 3:

km/sec

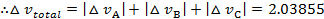km/sec b. Total transfer time,

where,

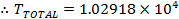sec

hr From Example 9-4, Hohmann Transfer only requires 0.9943 hr to transfer the spacecraft into another orbit. However, the bi-elliptic requires 3 times longer of transfer time to transfer the spacecraft into another orbit.

Date: 2016-04-22; view: 1029

<== previous page	\|	next page ==>
Tangential-Orbit Maneuver	\|	General Coplanar Transfer between Circular Orbits

doclecture.net - lectures - 2014-2024 year. Copyright infringement or personal data (0.005 sec.)