Combining relations

Since relations from A to B are subsets of 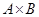, two relations from A to B can be combined in any way two sets can be combined.

Example. Let A = {1, 2, 3} and B = {1, 2, 3, 4}. The relations R₁ = {(1, 1), (2, 2), (3, 3)} and R₂ = {(1, 1), (1, 2), (1, 3), (1, 4)} can be combined to obtain , , .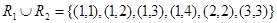

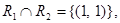
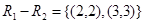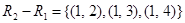There is another way that relations are combined which is analogous to the composition of functions.

Let R be a relation from a set A to a set B and S a relation from B to a set C. The composite of R and S is the relation consisting of ordered pairs (a, c), where , and for which there exists an element 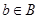such that 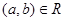and . We denote the composite of R and S by .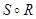

Example. What is the composite of the relations R and S where R is the relation from {1, 2, 3} to {1, 2, 3, 4} with R = {(1, 1), (1, 4), (2, 3), (3, 1), (3, 4)} and S is the relation from {1, 2, 3, 4} to {0, 1, 2} with S = {(1, 0), (2, 0), (3, 1), (3, 2), (4, 1)}?

Solution: 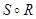is constructed using all ordered pairs in R and ordered pairs in S, where the second element of the ordered pair in R agrees with the first element of the ordered pair in S. For example, the ordered pair (2, 3) in R and (3, 1) in S produce the ordered pair in S. For example, the ordered pair (2, 3) in R and (3, 1) in S produce the ordered pair (2, 1) in 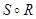. Computing all the ordered pairs in the composite, we find .

The powers of a relation R can be inductively defined from the definition of a composite of two relations.

Let R be a relation on the set A. The powers Rⁿ, n = 1, 2, 3, … are defined inductively by R¹ = R and 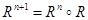. The definition shows that 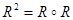, , and so on.

Example. Let R = {(1, 1), (2, 1), (3, 2), (4, 3)}. Find the powers Rⁿ, n = 2, 3, 4, …

Solution: Since 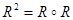, we find that 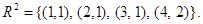Furthermore, since 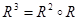, 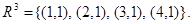Additional computation shows that R⁴ is the same as R³, so It is also follows that 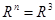for n = 5, 6, 7, …

Theorem 1. The relation R on a set A is transitive iff 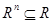for n = 1, 2, 3, …

n-ary relations

Let A₁, A₂, …, A_n be sets. An n-ary relation on these sets is a subset of 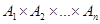. The sets A₁, A₂, …, A_n are called the domains of the relation, and n is called its degree.

Example. Let R be the relation consisting of triples (a, b, c), where a, b and c are integers with a < b < c. Then 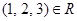, but 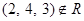. The degree of this relation is 3. Its domains are all equal to the set of integers.

Example. Let R be the relation consisting of 5-tuples (A, N, S, D, T) representing airplane flights, where A is the airline, N is the flight number, S is the starting point, D is the destination, and T is the departure time. For instance, if Nadir Express Airplanes has flight 963 from Newark to Bangor at 15:00, then (Nadir, 963, Newark, Bangor, 15:00) belongs to R. The degree of this relation is 5, and its domains are the set of all airlines, the set of flight numbers, the set of cities, the set of cities (again), and the set of times.

Date: 2015-01-02; view: 1438