Representing relations using matrices

A relation between finite sets can be represented using a zero-one matrix. Suppose that R is a relation from 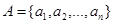to 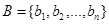. The relation R can be represented by the matrix 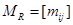, where .

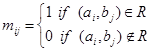In other words, the zero-one matrix representing R has a 1 as its (i, j) entry when a_i is related to b_j, and a 0 in this position if a_i is not related to b_j.

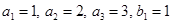Example. Suppose that A = {1, 2, 3} and B = {1, 2}. Let R be the relation from A to B containing (a, b) if and a > b. What is the matrix representing R if and ?

Solution: Since 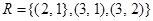, the matrix for R is .

Example. Let 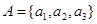and . Which ordered pairs are in the relation R represented by the matrix ?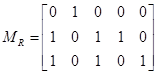

Solution: Since R consists of those ordered pairs with , it follows that R = {(a₁, b₂), (a₂, b₁),(a₂, b₃), (a₂, b₄), (a₃, b₁), (a₃, b₃), (a₃, b₅)}.

Representing relations using digraphs

A directed graph, or digraph, consists of a set V of vertices (or nodes) together with a set E of ordered pairs of elements of V called edges (or arcs). The vertex a is called the initial vertex of the edge (a, b), and the vertex b is called the terminal vertex of this edge.

An edge of the form (a, a) is represented using an arc from the vertex a back to itself. Such an edge is called a loop.

Example. The directed graph with vertices a, b, c and d, and edges (a, b), (a, d), (b, b), (b, d), (c, a), (c, b) and (d, b) is displayed in Figure: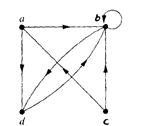

Example. The directed graph of the relation R = {(1, 1),(1, 3), (2, 1),(2, 3),(2, 4), (3, 1), (3, 2),(4, 1)} on the set {1, 2, 3, 4} is shown in Figure: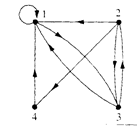

Example. What are the ordered pairs in the relation R represented by the directed graph shown in Figure below?

Solution: The ordered pair (x, y) in the relation are R = {(1, 3),(1, 4), (2, 1),(2, 2),(2, 3), (3, 1), (3, 3), (4, 1), (4, 3)}. Each of these pairs corresponds to an edge of the directed graph, with (2, 2) and (3, 3), corresponding to loops.

Glossary

composite –композиция;power –степень;directed graph –ориентированный граф

vertex –вершина;edge –ребро;loop –цикл

Date: 2015-01-02; view: 1451