
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Relations and their properties
Example. How many different strings can be made by reordering the letters of the word SUCCESS?
Solution: Because some of the letters of SUCCESS are the same, the answer is not given by the number of permutations of seven letters. This word contains three Ss, two Cs, one U, and one E. To determine the number of different strings that can be made by reordering the letters, first note that the three Ss can be placed among the seven positions in C(7, 3) different ways, leaving four positions free. Then the two Cs can be placed in C(4, 2) ways, leaving two free positions. The U can be placed in C(2, 1) ways, leaving just one position free. Hence E can be placed in C(1, 1) way. Consequently, from the product rule, the number of different strings that can be made is
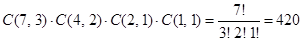 .
.
Theorem 6. The number of different permutations of n objects, where there are n1 indistinguishable objects of type 1, n2 indistinguishable objects of type 2, Е, and nk indistinguishable objects of type k, is  .
.
Glossary
permutation Ц перестановка; arrangement Ц размещение, расположение
saleswoman Ц продавщица; expansion Ц разложение; repetition Ц повторение
to allow Ц позвол€ть, разрешать; constraint Ц ограничение; combination Цсочетание
Relations and their properties
Let A and B be sets. A binary relation from A to B is a subset of 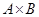 . In other words, a binary relation from A to B is a set R of ordered pairs where the first element of each ordered pair comes from A and the second element comes from B. We use the notation aRb to denote that (a, b) Î R and
. In other words, a binary relation from A to B is a set R of ordered pairs where the first element of each ordered pair comes from A and the second element comes from B. We use the notation aRb to denote that (a, b) Î R and  to denote that (a, b) Ï R. Moreover, when (a, b) belongs to R, a is said to be related to b by R. Binary relations represent relationships between the elements of two sets. We will omit the word УbinaryФ when there is no danger of confusion.
to denote that (a, b) Ï R. Moreover, when (a, b) belongs to R, a is said to be related to b by R. Binary relations represent relationships between the elements of two sets. We will omit the word УbinaryФ when there is no danger of confusion.
Example. Let A be the set of all cities, and let B be the set of the 50 states in the USA. Define the relation R by specifying that (a, b) belongs to R if city a is in state b. For instance, (Boulder, Colorado), (Chicago, Illinois), (Cupertino, California) are in R, but (Chicago, Colorado), (Cupertino, Illinois) are not in R.
Functions as relations.Recall that a function f from a set A to a set B assigns a unique element of B to each element of A. The graph of f is the set of ordered pairs (a, b) such that b = f(a). Since the graph of f is a subset of 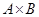 , it is a relation from A to B. Moreover, the graph of a function has the property that every element of A is the first element of exactly one ordered pair of the graph. Conversely, if R is a relation from A to B such that every element in A is the first element of exactly one ordered pair of R, then a function can be defined with R as its graph. This can be done by assigning to an element a of A the unique element
, it is a relation from A to B. Moreover, the graph of a function has the property that every element of A is the first element of exactly one ordered pair of the graph. Conversely, if R is a relation from A to B such that every element in A is the first element of exactly one ordered pair of R, then a function can be defined with R as its graph. This can be done by assigning to an element a of A the unique element 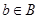 such that (a, b) Î R.
such that (a, b) Î R.
Relations on a set
A relation on the set A is a relation from A to A. In other words, a relation on a set A is a subset of 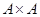 .
.
Example. Let A = {1, 2, 3, 4}. Which ordered pairs are in the relation R = {(a, b) | a divides b}?
Solution: R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 4), (3, 3), (4, 4)}.
Example. Consider the following relations on the set of integers:
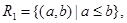

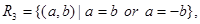
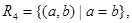
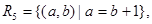

Which of these relations contain each of the pairs (1, 1), (1, 2), (2, 1), (1, Ц1) and (2, 2)?
Solution: The pair (1, 1) is in R1, R3, R4, and R6; (1, 2) is in R1 and R6; (2, 1) is in R2, R5 and R6; (1, Ц1) is in R2, R3 and R6; and finally, (2, 2) is in R1, R3 and R4.
Example. How many relations are there on a set with n elements?
Solution: A relation on a set A is a subset of 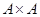 . Since
. Since 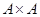 has n2 elements when A has n elements, and a set with m elements has 2m subsets, there are
has n2 elements when A has n elements, and a set with m elements has 2m subsets, there are  subsets of
subsets of 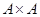 . Thus, there are
. Thus, there are  relations on a set with n elements.
relations on a set with n elements.
Properties of relations
A relation R on a set A is called reflexive if (a, a) Î R for every element  .
.
Example 1. Consider the following relations on {1, 2, 3, 4}: R1 = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 4), (4, 1), (4, 4)}, R2 = {(1, 1), (1, 2), (2, 1)}, R3 = {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (3, 3), (4, 1), (4, 4)}, R4 = {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3)}, R5 = {(1, 1), (1, 2), 91, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)}, R6 = {(3, 4)}. Which of these relations are reflexive?
Example. Is the УdividesФ relation on the set of positive integers reflexive?
Solution: Since a | a whenever a is a positive integer, the УdividesФ relation is reflexive.
A relation R on a set A is called symmetric if  whenever
whenever 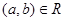 , for
, for  A relation R on a set A such that
A relation R on a set A such that 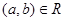 and
and  only if a = b, for
only if a = b, for 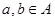 , is called antisymmetric.
, is called antisymmetric.
The terms symmetric and antisymmetric are not opposites, since a relation can have both of these properties or may lack both of them. A relation cannot be both symmetric and antisymmetric if it contains some pair of the form (a, b) where a ¹ b.
Example. Which of the relations from Example 1 are symmetric and which are antisymmetric?
Solution: The relations R3, R4 and R6 are symmetric, for if  or
or  , then
, then 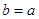 or
or  . R4 is symmetric since a = b implies that
. R4 is symmetric since a = b implies that 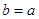 . R6 is symmetric since
. R6 is symmetric since 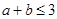 implies that
implies that 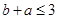 .
.
The relations R1, R2, R4 and R5 are antisymmetric.
Example. Is the УdividesФ relation on the set of positive integers symmetric? Is it antisymmetric?
Solution: This relation is not symmetric since 1 | 2, but 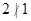 . It is antisymmetric, for if a and b are positive integers with a | b and b | a, then a = b.
. It is antisymmetric, for if a and b are positive integers with a | b and b | a, then a = b.
A relation R on a set A is called transitive if whenever 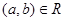 and
and 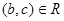 , then
, then  , for
, for 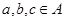 .
.
Example. Which of the relations in Example 1 are transitive?
Solution: R4, R5 and R6 are transitive.
Example. Is the УdividesФ relation on the set of positive integers transitive?
Solution: Suppose that a divides b and b divides c. Then there are positive integers k and l such that b = ak and c = bl. Hence, c = akl, so that a divides c. It follows that this relation is transitive.
Date: 2015-01-02; view: 2310
| <== previous page | | | next page ==> |
| Permutations of sets with indistinguishable objects | | | Combining relations |