Permutations of sets with indistinguishable objects

Example. How many different strings can be made by reordering the letters of the word SUCCESS?

Solution: Because some of the letters of SUCCESS are the same, the answer is not given by the number of permutations of seven letters. This word contains three Ss, two Cs, one U, and one E. To determine the number of different strings that can be made by reordering the letters, first note that the three Ss can be placed among the seven positions in C(7, 3) different ways, leaving four positions free. Then the two Cs can be placed in C(4, 2) ways, leaving two free positions. The U can be placed in C(2, 1) ways, leaving just one position free. Hence E can be placed in C(1, 1) way. Consequently, from the product rule, the number of different strings that can be made is

.

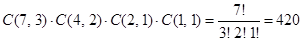Theorem 6. The number of different permutations of n objects, where there are n₁ indistinguishable objects of type 1, n₂ indistinguishable objects of type 2, …, and n_k indistinguishable objects of type k, is .

Glossary

permutation – перестановка; arrangement – размещение, расположение

saleswoman – продавщица; expansion – разложение; repetition – повторение

to allow – позволять, разрешать; constraint – ограничение; combination –сочетание

Date: 2015-01-02; view: 1160