Combinations with repetition

Example. How many ways are there to select four pieces of fruit from a bowl containing apples, oranges, and pears if the order in which the pieces are selected does not matter, only, the type of fruit and not the individual piece matters, and there are at least four pieces of each type of fruit in the bowl?

Solution: To solve this problem we list all the ways possible to select the fruit. There are 15 ways: 4 apples; 4 oranges; 3 apples, 1 orange; 3 oranges, 1 pear; …; 2 oranges, 2 pears; 2 pears, 1 apple, 1 orange. The solution is the number of 4-combinations with repetition allowed from a three-element set {apple, orange, pear}.

Theorem 5. There are C(n + r – 1, r) r-combinations from a set with n elements when repetition of elements is allowed.

Proof: Each r-combination of a set with n elements when repetition is allowed can be represented by a list of n – 1 bars and r stars. The n – 1 bars are used to mark off n different cells, with the i^th cell containing a star for each time the i^th element of the set occurs in the combination. For instance, a 6-combination of a set with four elements is represented with three bars and six stars.

Here * * | * | | * * * represents the combination containing exactly two of the first element, one of the second element, none of the third element, and three of the fourth element of the set.

As we have seen, each different list containing n – 1 bars and r stars corresponds to an r-combination of the set with n elements, when repetition is allowed. The number of such lists is C(n – 1 + r, r), since each list corresponds to a choice of the r positions to place the r stars from the n – 1 + r positions that contain r stars and n – 1 bars.

Example. Suppose that a cookie shop has four different kinds of cookies. How many different ways can six cookies be chosen? Assume that only the type of cookie, and not the individual cookies or the order in which they are chosen, matters.

Solution: The number of ways to choose six cookies is the number of 6-combinations of a set with four elements. From Theorem 5 this equals C(4 + 6 – 1, 6) = C(9, 6). Since C(9, 6) = 84, there are 84 different ways to choose the six cookies.

Example. How many solutions does the equation 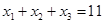have, where x₁, x₂ and x₃ are nonnegative integers?

Solution: To count the number of solutions, we note that a solution corresponds to a way of selecting 11 items from a set with three elements, so that x₁ items of type one, x₂ items of type two, and x₃ items of type three are chosen. Hence, the number of solutions is equal to the number of 11-combinations with repetition allowed from a set with three elements. Form Theorem 5 it follows that there are solutions.

The number of solutions of this equation can also be found when the variables are subject to constraints. For instance, we can find the number of solutions where the variables are integers with , 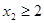and 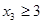. A solution to the equation subject to these constraints corresponds to a selection of 11 items with x₁ items of type one, x₂ items of type two, and x₃ items of type three, where, in addition, there is at least one item of type one, two items of type two, and three items of type three. So, choose one item of type one, two of type two, and three of type three. Then select five additional items. By Theorem 5 this can be done in 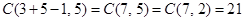ways.

Date: 2015-01-02; view: 1220