CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
The binomial theorem
The binomial theorem gives the coefficients of the expansion of powers of binomial expressions. A binomial expression is simply the sum of two terms, such as x + y.
Example. The expansion of 
can be found using combinatorial reasoning instead of multiplying the three terms out. When 
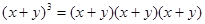is expanded, all products of a term in the first sum, a term in the second sum, and a term in the third sum added. Terms of the form x3, x2y, xy2, and y3 arise. To obtain a term of the form x3, an x must be chosen in each of the sums, and this can be done in only one way. Thus, the x3 term in the product has a coefficient of 1. To obtain a term of the form x2y, an x must be chosen in two of the three sums (and consequently a y in the other sum). Hence, the number of such terms is the number of 2-combinations of three objects, namely C(3, 2). Similarly, the number of terms of the form xy2 is the number of ways to pick one of the three sums to obtain an x (and consequently take a y from each of other two terms). This can be done in C(3, 1) ways. Finally, the only way to obtain a y3 term is to choose the y for each of the three sums in the product, and this can be done in exactly one way. Consequently, it follows that 
Theorem 3 (the binomial theorem). Let x and y be variables, and let n be a positive integer. Then
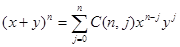
Proof: The terms in the product when it is expanded are of the form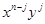 
for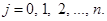 
To count the number of terms of the form 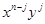, note that to obtain such a term it is necessary to choose n – j xs from the n sums (so that the other j terms in the product are ys). Therefore, the coefficient of 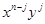is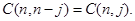 
Example. What is the expansion of 
?
Solution: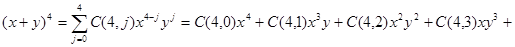 
.
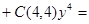
Example. What is the coefficient of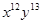 
in the expansion of 
?
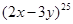Solution: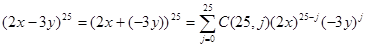 
. Consequently, the coefficient of 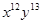in the expansion is obtained when j = 13, namely, 
.
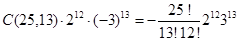Permutations with repetition
Example. How many strings of length n can be formed from the English alphabet?
Solution: By the product rule, since there are 26 letters, and since each letter can be used repeatedly, we see that there are 26n strings of length n.
Theorem 4. The number of r-permutations of a set of n objects with repetition allowed is nr.
Proof: There are n ways to select an element of the set for each of the r positions in the r-permutation when repetition is allowed, since for each choice all n objects are available. Hence, by the product rule there are nr r-permutations when repetition is allowed.
Date: 2015-01-02; view: 1254
| <== previous page | | | next page ==> |
| Combinations | | | Combinations with repetition |