Combinations

An r-combination of elements of a set is an unordered selection of r elements from the set. Thus, an r-combination is simply a subset of the set with r elements.

Example. Let S be the set {1, 2, 3, 4}. Then {1, 3, 4} is a 3-combination from S.

The number of r-combinations of a set with n distinct elements is denoted by C(n, r).

Example. We see that C(4, 2) = 6, since the 2-combinations of {a, b, c, d} are the six subsets {a, b}, {a, c}, {a, d}, {b, c}, {b, d}, and {c, d}.

We can determine the number of r-combinations of a set with n elements using the formula for the number of r-permutations of a set. To do this, note that the r-permutations of a set can be obtained by first forming r-combinations and then ordering the elements in these combinations.

Theorem 2. The number of r-combinations of a set with n elements, where n is a positive integer and r is an integer with 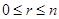, equals .

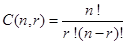Proof: The r-permutations of the set can be obtained by forming the C(n, r) r-combinations of the set, and then ordering the elements in each r-combination, which can be done in P(r, r) ways. Consequently, 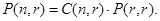This implies that .

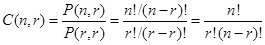Corollary 1. Let n and r be nonnegative integers with 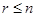. Then .

There is another common notation for the number of r-combinations from a set with n elements, namely, 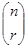, i.e. 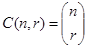. This number is also called a binomial coefficient. The name “binomial coefficient” is used because these numbers occur as coefficients in the expansion of powers of binomial expressions such as .

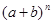Example. How many ways are there to select 5 players from a 10-member tennis team to make a trip to a match at another school?

Solution: The answer is given by the number of 5-combinations of a set with 10 elements:

Example. How many ways are there to select a committee to develop a discrete mathematics course at a school if the committee is to consist of 3 faculty members from the mathematics department and 4 from the computer science department, if there are 9 faculty members of the mathematics department and 11 of the computer science department?

Solution: By the product rule, the answer is the product of the number of 3-combinations of a set with 9 elements, and the number of 4-combinations of a set with 11 elements.

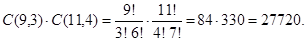
Date: 2015-01-02; view: 1004