Permutations

The For-to-Infinitive Construction is a construction in which the Infinitive is in predicate relation to a noun or pronoun preceded by the preposition “for”.

In translating this construction into Russian a subordinate clause or an infinitive is used. The construction can have different functions in the sentence. It can be:

Subject, often with the introductory “it”

Eg. I sometimes think it is shame for people to spend so much money this way. – Я иногда думаю, что стыдно людям тратить на это

так много денег.

Predicative

Eg. That was for him to find out. – Выяснить это должен был он.

Attribute

Eg. There is nobody here for him to play with. – Здесь нет никого,

скем он мог бы поиграть.

Complex Object

Eg. He waited for her to speak. – Он ждал, когда она заговорит.

He asked for the papers to be brought. – Он попросил принести

бумаги.

Adverbial Modifier:

of result

Eg. He spoke loud enough for you to hear. – Он говорил достаточно

громко, чтобы Вы могли его слышать.

He had consented, and it was too late for him now to recede. – Он уже

дал согласие, и теперь было поздно отступать.

of purpose

Eg. He stepped aside for me to pass. – Он отошел в сторону, чтобы я могла пройти.

He spoke loud for me to hear. – Он говорил громко, чтобы я могла услышать.

With the expressions “to be sorry”, “to be glad”, “to be pleased” the Infinitive is used only if the subject of the sentence represents at the same time the doer of the action expressed by the Infinitive, over wise a subordinate clause is used.

Eg. I am pleased to have got a ticket for the concert. – Я рада, что достала билет на этот концертю

I am glad to have seen you. – Я раг, что встретил тебя.

I am glad you got a ticket for the concert. – Я рад, что Вы достали билет на этот концерт.

IV. The Absolute Infinitive Construction

The subject of the infinitive in all adverbial functions is the same person or thing as denoted by the subject of the sentence. But the Infinitive may also have a subject of its own with which it forms the so-called Absolute Construction with the Infinitive.

The Absolute Construction with the Infinitive is introduced by the preposition “with”. The Infinitive is used with the particle “to”.

The Absolute Construction with the Infinitive has the function of adverbial modifier of attending circumstances in the sentence.

Eg. Miss Jillian is bellow, Sir, with a carriage to take you home. – Сэр, мисс Джиллиан находится внизу, с экипажем, который отвезет Вас домой.

There are two parallel actions in this sentence. One of them is expressed by the predicate, the other – by the Infinitive. Each action has its own subject.

The Infinitive Absolute Construction is infrequent and found only in literary style.

Permutations

A permutation of a set of distinct objects is an ordered arrangement of these objects.

An ordered arrangement of r elements of a set is called an r-permutation.

Example. Let S = {1, 2, 3}. The arrangement 3, 1, 2 is a permutation of S. The arrangement 3, 2 is a 2-permutation of S.

The number of r-permutations of a set with n elements is denoted by P(n, r).

Theorem 1. The number of r-permutations of a set with n distinct elements is

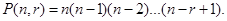
Proof: The first element of the permutation can be chosen in n ways, since there are n elements in the set. There are n – 1 ways to choose the second element of the permutation, since there are n – 1 elements left in the set after using the element picked for the first position. Similarly, there are n – 2 ways to choose the third element, and so on, until there are exactly n – r + 1 ways to choose the r^th element. Consequently, by the product rule, there are 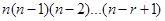r-permutations of the set. ;

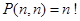
Example. How many different ways are there to select 4 different players from 10 players on a team to play four tennis matches, where the matches are ordered?

Solution: The answer is given by the number of 4-permutations of a set with 10 elements. By Theorem 1, this is P(10, 4) = 10 × 9 × 8 × 7 = 5040.

Example. Suppose that a saleswoman has to visit eight different cities. She must begin her trip in a specified city, but she can visit the other seven cities in any order she wishes. How many possible orders can the saleswoman use when visiting these cities?

Solution: The number of possible paths between the cities is the number of permutations of seven elements, since the first city is determined, but the remaining seven can be ordered arbitrarily. Consequently, there are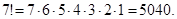

Date: 2015-01-02; view: 1336