Bipartite graphs

A simple graph G is called bipartite if its vertex set V can be partitioned into two disjoint nonempty sets V₁ and V₂ such that every edge in the graph connects a vertex in V₁ and a vertex in V₂ (so that no edge in G connects either two vertices in V₁ or two vertices in V₂).

Example. C₆ is bipartite since its vertex set can be partitioned into the two sets 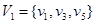and 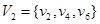, and every edge of C₆ connects a vertex in V₁ and a vertex in V₂.

Example. K₃ is not bipartite. To see this, note that if we divide the vertex set of K₃ into two disjoint sets, one of the two sets must contain two vertices. If the graph were bipartite, these two vertices could not be connected by an edge, but in K₃ each vertex is connected to every other vertex by an edge.

Example. Are the graphs G and H bipartite?

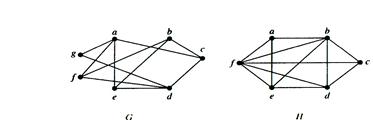
Solution: Graph G is bipartite, since its vertex set is the union of two disjoint sets {a, b, d} and {c, e, f, g}, and each edge connects a vertex in one of these subsets to a vertex in the other subset. Note that for G to be bipartite it is not necessary that every vertex in {a, b, d} be adjacent to every vertex in {c, e, f, g}. For instance, b and g are not adjacent.

Graph H is not bipartite since its vertex set cannot be partitioned into two subsets so that edges do not connect two vertices from the same subset.

Example. The complete bipartite graph 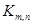is the graph that has its vertex set partitioned into two subsets of m and n vertices, respectively. There is an edge between two vertices iff one vertex is in the first subset and the other vertex is in the second subset.

Date: 2015-01-02; view: 1100